Question

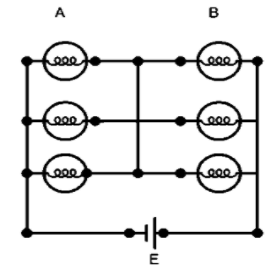
Six similar bulbs are connected as shown in the figure to a DC source of electromotive force E and a zero internal resistance. The ratio of the power consumption by the bulbs when all the bulbs are glowing to when the two from A and one from B are glowing is given by –

A) 2:1
B) 4:9
C) 9:4
D) 1:2

Answer 1

We are given a combination of bulbs connected in series and parallel to each other connected to an external source. We can find the power consumption ratios of the bulb combinations at the given conditions using the relation between the voltage and the resistance of the bulbs.

Complete answer:
We know that the bulbs in a circuit constitute the loads or the resistances in the network. We can easily approach this given situation with this idea.
Here, six bulbs of equal resistance are connected as given below. Each bulb offers resistance of ‘R’. We need to find the equivalent resistance of the circuit by including the bulbs which glow in a given condition.

CASE I: All the bulbs are glowing. In this case, we can easily consider the bulbs in A as parallel to each other and in series to the ones in B.
So, the parallel bulbs combination can be given as –

& \dfrac{1}{{{R}_{A}}}=\dfrac{1}{{{R}_{B}}}=\dfrac{1}{R}+\dfrac{1}{R}+\dfrac{1}{R}=\dfrac{3}{R} \\\ & {{R}_{A}}={{R}_{B}}=\dfrac{R}{3} \\\ \end{aligned}$$ Now, the equivalent resistance can be given as – $${{R}_{eq}}={{R}_{A}}+{{R}_{B}}=\dfrac{2R}{3}$$ The power consumed in the network in this case is given by – $$\begin{aligned} & P=\dfrac{{{E}^{2}}}{{{R}_{eq}}} \\\ & {{P}_{1}}=\dfrac{3{{E}^{2}}}{2R}\text{ --(1)} \\\ \end{aligned}$$ CASE II: Two bulbs in section A and one bulb in section B glows. We can simplify the circuit as shown below.  The equivalent resistance is given by – $$\begin{aligned} & \dfrac{1}{{{R}_{A}}}=\dfrac{1}{R}+\dfrac{1}{R}=\dfrac{2}{R} \\\ & \Rightarrow {{R}_{A}}=\dfrac{R}{2} \\\ & {{R}_{B}}=R \\\ & {{R}_{eq}}={{R}_{A}}+{{R}_{B}}=\dfrac{3R}{2} \\\ \end{aligned}$$ Now, we can calculate the power dissipation in the network as – $$\begin{aligned} & P=\dfrac{{{E}^{2}}}{{{R}_{eq}}} \\\ & {{P}_{2}}=\dfrac{2{{E}^{2}}}{3R}\text{ --(2)} \\\ \end{aligned}$$ We require to find the ratio of power consumptions in case I and case II. This is considered by taking the ratios of (1) and (2) as - $$\dfrac{{{P}_{1}}}{{{P}_{2}}}=\dfrac{\dfrac{3{{E}^{2}}}{2R}}{\dfrac{2{{E}^{2}}}{3R}}=\dfrac{9}{4}$$ The ratio of the power consumption for the two conditions I and II are given by 9:4. **The correct answer is option C.** **Note:** The power consumed by the electrical devices is not only dependent on its individual resistances, but is also dependent on the type of combination the circuit is designed. This is an important criterion to be considered while designing a circuit to avoid unnecessary loss of current.