Question
Question: Six rods of the same mass m and length l are arranged as shown in figure. Calculate the coordinate o...
Six rods of the same mass m and length l are arranged as shown in figure. Calculate the coordinate of the centre of mass of system:
A.(\dfrac{L}{2},\dfrac{{7L}}{6}) \\\
B.(\dfrac{L}{2},L) \\\
C.(\dfrac{L}{2},\dfrac{{4L}}{3}) \\\
D.(\dfrac{L}{2},\dfrac{{5L}}{3}) \\\
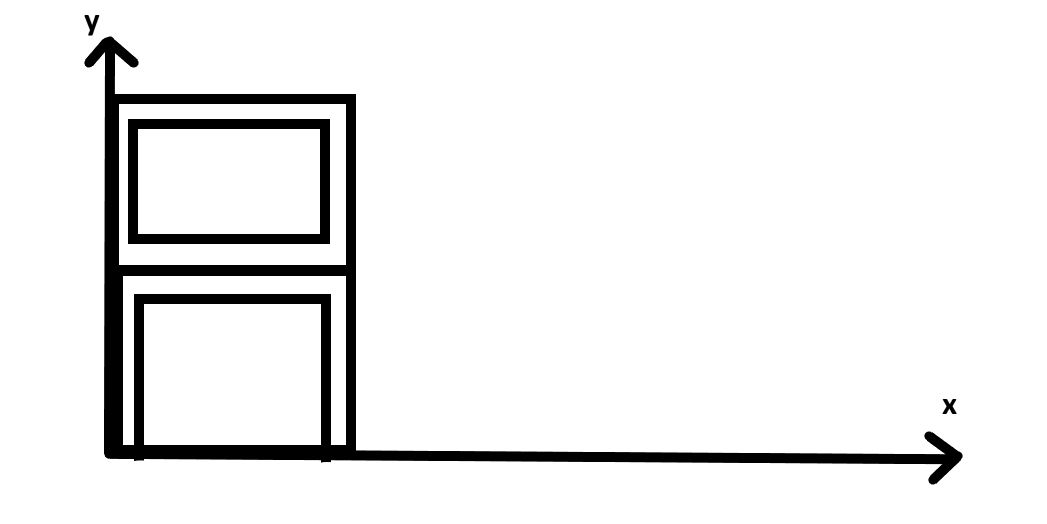
Solution
Hint : In order to solve this question first we have to find the midpoint of the rods. After this we have to locate the coordinate of these points. After locating these points we find for the X CM and Y CM respectively by the formula.
Complete Step By Step Answer:
As we know that the centre of mass of anybody lies on its centre, here in the rod centre of mass lies a rod of length l lying with a distance of 2l from the corner.
Now we are going to write the coordinate of each point in the figure.
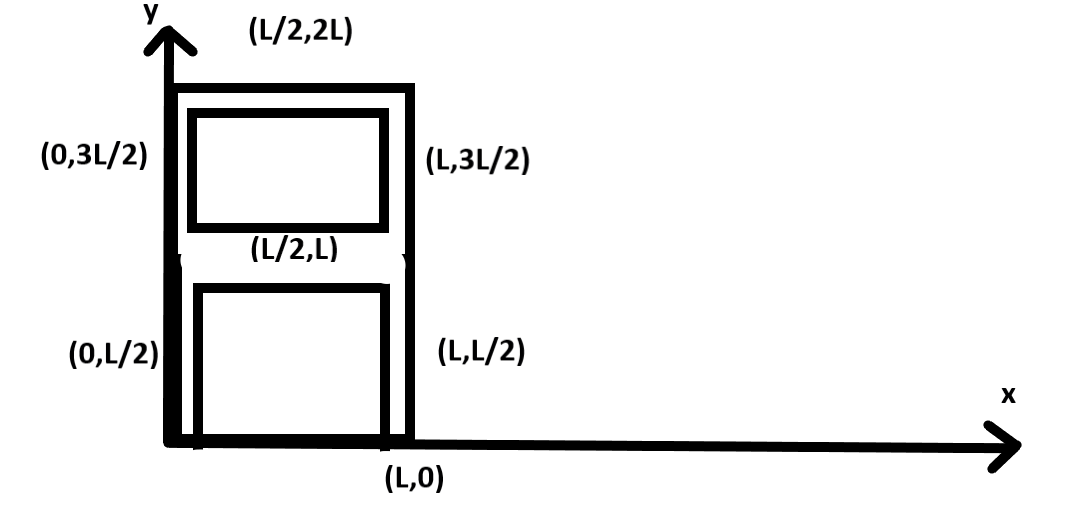
Here Xcm is the mean of the centre of mass of all rods. So;
Xcm=6mmx1+mx2+mx3+mx4+mx5+mx6
Taking common m we got;
{X_{cm}} = \dfrac{{{x_1} + {x_2} + {x_3} + {x_4} + {x_5} + {x_6}}}{6} \\\
\\\
Putting the values of x coordinate from the figure,
{X_{cm}} = \dfrac{{0 + 0 + \dfrac{L}{2} + \dfrac{L}{2} + L + L}}{6} \\\
= \dfrac{{3L}}{6} \\\
= \dfrac{L}{2} \\\
Calculating the Ycm of the rod,
Ycm=6mmy1+my2+my3+my4+my5+my6
Taking common m we got;
Ycm=6y1+y2+y3+y4+y5+y6
Putting the values of y coordinate from the figure,
{X_{cm}} = \dfrac{{\dfrac{L}{2} + \dfrac{{3L}}{2} + L + 2L + \dfrac{L}{2} + \dfrac{{3L}}{2}}}{6} \\\
= \dfrac{{7L}}{6} \\\
Then the coordinate for the system is (2L,67L) .
Hence option A is the correct answer.
Note :
The centre of mass is a position defined relative to an object or at the given system of an object. If we are talking about the solid objects having uniform density, the centre of mass is called the centroid. It is the point where any uniform force on the objects act.
It can be calculated by taking the masses we are putting to find the centre of mass between multiplying them by their position.
