Question
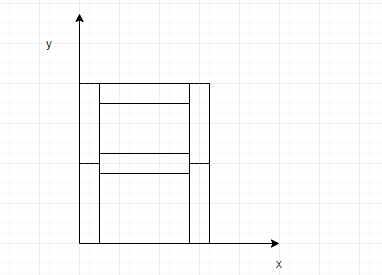
Question: Six rods of the same mass m and length \(l\)are arranged as shown in figure. Calculate the coordinat...
Six rods of the same mass m and length lare arranged as shown in figure. Calculate the coordinate of the centre of mass of the system
A. (2l,67l)
B. (3l,l)
C. (2l,34l)
D. (2l,35l)
Solution
We’re given six rods. The centre of mass of each rod lies at the midpoint. That is if the length is l, it is at a distance 2l. Further, we have to find the coordinates of all the centre of masses, that is the centre of mass of every individual rod, as each of it contributes to the overall centre of mass of the system.
Formula used:
Centre of mass of system: xcm=Mi=1∑Nmixi, where m is the mass and x is the distance
Complete step by step answer:
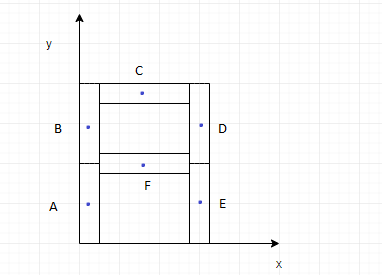
From the modified figure, we deduce that,
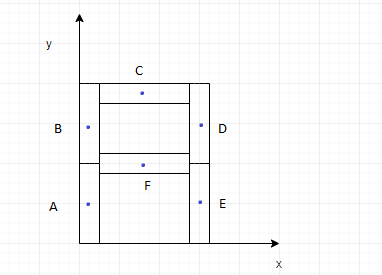
Coordinates of A: (0,2l)
Coordinates of B: (0,23l)
Coordinates of C: (2l,2l)
Coordinates of D: (l,23l)
Coordinates of E: (l,2l)
Coordinates of F: (2l,l)
Hence, we have found the coordinates of the centre of mass of each individual rod.
From the formula mentioned above,
Centre of mass of the system: xcm=6mmx1+mx2+mx3+mx4+mx5+mx6
=6x1+x2+x3+x4+x5+x6
Substituting the above calculated values,
xcm=60+0+2l+l+l+2l =63l=2l
Thus the value of the x coordinate is founded.
Similarly, ycm=6mmy1+my2+my3+my4+my5+my6
=6y1+y2+y3+y4+y5+y6
Substituting the above calculated values,
ycm=62l+23l+l+2l+2l+23l =67l.
Thus, the value of the y coordinate is founded.
Hence, the centre of mass of the entire system is at (2l,67l)
Note:
We can initially estimate the centre of mass by neglecting the horizontal rods.
Two parallel rods will have the centre of mass at the midpoint of the line joining their midpoints.
The contributions of the horizontal rods cause slight variation from this position.
