Question

Six point charges are placed at the vertices of a hexagon of side 1m as shown in figure. Net electric field at the centre of the hexagon is

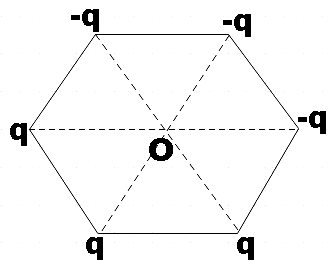
A. zero
B.$\dfrac{6q}{4\pi {{\varepsilon }_{0}}}$
C.$\dfrac{q}{\pi {{\varepsilon }_{0}}}$
D.$\dfrac{q}{4\pi {{\varepsilon }_{0}}}$

Answer 1

Firstly, you could find the electric field along the diagonal due to the two charges +q and –q kept at the two ends. Then you could consider any 2 of the 3 diagonals and then find vector sum of their respective electric fields. This resultant electric field will lie perpendicular to the third diagonal electric field. Again do the vector sum to find the net field at the centre of the given hexagon.
Formula used:
Electric field,
$E=\dfrac{kq}{{{r}^{2}}}$

Complete answer:
In the question, we are given six point charges placed at vertices of a hexagon of side 1m. We are supposed to find the net electric field at the centre of the hexagon.
Let us recall that, the electric field due to any charge q is given by,
$E=\dfrac{kq}{{{r}^{2}}}$ ……………………………………………………. (1)
In order to answer this question, we could consider each diagonal.

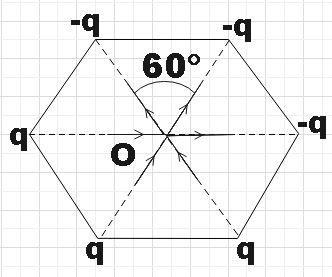
We see that the electric field along each diagonal is contributed by +q as well as –q.
So, the electric field along the diagonal is given by,
$E=\dfrac{kq}{{{1}^{2}}}+\dfrac{kq}{{{1}^{2}}}=2kq$
Each diagonal will have the same electric field along it.
Also, since we are given regular hexagon, we know that the angle between two diagonals will be$60{}^\circ$.
Now we could do vector addition to get the resultant electric field along two diagonals.
$E'=\sqrt{{{E}^{2}}+{{E}^{2}}+2{{E}^{2}}\cos \theta }$
$\Rightarrow E'=\sqrt{{{\left( 2kq \right)}^{2}}+{{\left( 2kq \right)}^{2}}+2{{\left( 2kq \right)}^{2}}\cos 60{}^\circ }=\sqrt{{{\left( 2kq \right)}^{2}}+{{\left( 2kq \right)}^{2}}+2{{\left( 2kq \right)}^{2}}\left( \dfrac{1}{2} \right)}$
$\Rightarrow E'=\sqrt{{{\left( 2kq \right)}^{2}}+{{\left( 2kq \right)}^{2}}+{{\left( 2kq \right)}^{2}}}=2\sqrt{3}kq$
This electric field will lie perpendicular to the other electric field, so, the net electric field would be,
${{E}_{net}}=\sqrt{{{\left( 2kq \right)}^{2}}+{{\left( 2\sqrt{3}kq \right)}^{2}}+2\left( 2kq \right)\left( 2\sqrt{3}kq \right)\cos 90{}^\circ }$
$\Rightarrow {{E}_{net}}=\sqrt{{{\left( 2kq \right)}^{2}}+{{\left( 2\sqrt{3}kq \right)}^{2}}}=2kq\sqrt{4}$
$\therefore {{E}_{net}}=4kq$
But we know that k is given by,
$k=\dfrac{1}{4\pi {{\varepsilon }_{0}}}$
$\Rightarrow {{E}_{net}}=\dfrac{4q}{4\pi {{\varepsilon }_{0}}}$
$\therefore {{E}_{net}}=\dfrac{q}{\pi {{\varepsilon }_{0}}}$
Therefore, we found the net electric field at the centre of the given hexagon to be,
${{E}_{net}}=\dfrac{q}{\pi {{\varepsilon }_{0}}}$

Hence, option C is the correct answer.

Note:
You may have noted that along the diagonal the net electric field taken as the sum of the electric field due to each charge at the end of the diagonals. Though it may appear that we have not considered the sign of the charge, it is not so. The direction of the electric field is opposite to that due to positive charge. So,
$E=\dfrac{kq}{{{1}^{2}}}+\left( -\dfrac{k\left( -q \right)}{{{1}^{2}}} \right)=2kq$