Question

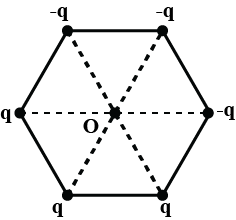
Six point charges are placed at the vertices of a hexagon of side 1 m as shown in figure. Net electric field at the center of the hexagon is

A. Zero
B. $\dfrac{{6q}}{{4\pi {\varepsilon _0}}}$
C. $\dfrac{q}{{\pi {\varepsilon _0}}}$
D. $\dfrac{q}{{4\pi {\varepsilon _0}}}$

Answer 1

In order to solve this numerical we should use the formula of resultant electric field such that we find the net electric field at the center of the hexagon.

Complete step by step answer:
According to the above diagram, we find each triangle is shown as an equilateral triangle which is a symmetrical hexagon.
We will consider each diagonal to calculate the electric field.
Hence total electric field is given by

\ {E_1} = {E_2} = E \\\ E = {E_1} + {E_2} \\\ \Rightarrow E = \dfrac{1}{{4\pi {\varepsilon _0}}}\dfrac{q}{{{r^2}}} + \dfrac{1}{{4\pi {\varepsilon_0}}}\dfrac{q}{{{r^2}}} \\\ \Rightarrow E = 2Kq \\\ \
Resultant electric field due to two diagonal making an angle at 60°
$\ {E_{net}} = \sqrt {{E^2} + {E^2} + 2{E^2}\cos \theta } \\\ \Rightarrow {E_{net}} = \sqrt {{{(2Kq)}^2} + {{(2Kq)}^2} + 2{E^2}\cos {{60}^0}} \\\ \Rightarrow {E_{net}} = \sqrt {{{(2Kq)}^2} + {{(2Kq)}^2} + {{(2Kq)}^2}} \\\ \Rightarrow {E_{net}} = \sqrt 3 (2Kq) \\\ \$
Let us consider, by calculating the net resultant electric field
\ {E_{net}} = \sqrt {{E_n}^2 + {E^2}} \\\ \Rightarrow {E_{net}} = \sqrt {{{(2Kq\sqrt 3 )}^2} + {{(2Kq)}^2}} \\\ \Rightarrow {E_{net}} = 2Kq\sqrt 4 \\\ \Rightarrow {E_{net}} = 4Kq \\\ \Rightarrow {E_{net}} = 4q\dfrac{1}{{4\pi {\varepsilon _0}}} \\\ \Rightarrow {E_{net}} = \dfrac{q}{{\pi {\varepsilon _0}}} \\\ \

Hence the correct option is C.

Note: Usually we refer to the surrounding space around an electric charge in which its influenced can is nothing but the electric field. The positive charge of an electric field intensity is always directed away from the charge and the negative charge of the intensity is always directed towards the charge.