Question
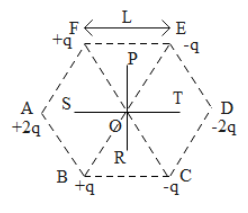
Question: Six point charges are kept at the vertices of a regular hexagon of side L and centre O, as shown in ...
Six point charges are kept at the vertices of a regular hexagon of side L and centre O, as shown in the figure. Given that K=4π∈01L2q, which of the following statement(s) is (are) correct?
This question has multiple correct options
A. The electric field at O is 6K along OD.
B. The potential at O is zero.
C. The potential at all points on the line PR is the same.
D. The potential at all points on the line ST is the same.
Solution
The electric potential can be calculated at point O by taking the vector sum of the electric fields due to various charges. The electric potential is a scalar quantity and its resultant is obtained by simply adding the potentials due to the charges.
Complete answer:
We are given six point charges which are kept at the vertices of a regular hexagon of side L and centre O. The electric field due to +q charge is given as
K=4π∈01L2q
Similarly we have an electric field due to –q charge which can be given as –K, for the charge +2q, the value of electric field is +2K; for charge -2q, the value of electric field is -2K.
As we know that electric field is a vector quantity, in order to obtain the resultant of these electric fields at point O, we need to perform vector addition.
The direction of the electric field is always from positive to negative charge. Therefore, we can represent directions of electric fields in the diagram in the following way. The resultant is directed in the direction of OD.

The resultant electric field at O is given as
E=+K−(−K)+2K−(−2K)+K−(−K)=6K
Hence, the resultant electric field is 6K at O.
For the case of potential, we need to add up the charges to obtain the net charge and then insert the net value into the formula for potential.
Net charge =+q−q+2q−2q+q−q=0
Since net charge is zero, the net potential at O is also zero.
V=4π∈01Lqnet=0
Hence, we can say that the correct answers are options A and B.
Note:
To avoid confusion between the methods used to obtain the net electric field and the electric potential, the students should remember the direction of electric field due to positive and negative charges in case of electric field. For electric potential, only the sign of the charges needs to be taken into consideration.
