Question

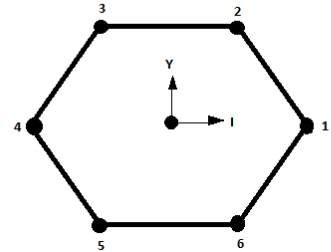
Six objects are placed at the vertices of a regular hexagon. The geometric center of the hexagon is at the origin with objects $1$ and $4$ on the x-axis (see figure). The mass of the ${k^{th}}$object is ${m_k} = {k^i}M\left| {cos{\theta _k}} \right|$where $i$ is an integer, M is a constant with dimension of mass, and ${\theta _k}$ is the angular position of the ${k^{th}}$ vertex measured from the positive x-axis in the counterclockwise sense. If the net gravitational force on a body at the centroid vanishes, the value of $i$ is?

$\left( {{A}} \right){{ 0}}$
$\left( {{B}} \right){{ }}1$
$\left( {{C}} \right){{ 2}}$
$\left( {{D}} \right){{ }}3$

Answer 1

Here, net gravitational force is zero then the forces from the opposite side of the object cancel out.
According to the question we have ,
net gravitational force is equal to zero.
mass of ${k^{th}}$object is ${m_k} = {k^i}M\left| {cos{\theta _k}} \right|$

Complete step by step answer:
When the net gravitational force is zero then the diagonal opposite vertices of the hexagon should be equal to each other. So, depending upon this theory we will have $3$ conditions.
${m_1} = {{ }}{m_4},{{ }}{m_2} = {{ }}{m_5},{{ }}{m_3} = {{ }}{m_6}$
We can take any one condition to get the value of I.
Let us take ${m_1} = {{ }}{m_4}$
${{{k}}^{{i}}}{{M}}\mid {{cos}}{{{\theta }}_{{k}}}{\mid _{{{k = 1}}}} = {{{k}}^{{i}}}{{M}}\mid {{cos}}{{{\theta }}_{{k}}}{\mid _{{{k = 4}}}}$
The value of ${{{\theta }}_{{1}}} = 0$ and value of ${{{\theta }}_2} = 180$
By substituting we have,
$\Rightarrow {1^{{i}}}|\cos {{{\theta }}_1}| = {4^{{i}}}|\cos {{{\theta }}_4}|$.
$\Rightarrow {1^{{i}}}\cos {0^ \circ } = {4^{{i}}}\cos {180^ \circ }$
Here, $\cos {0^ \circ } = \cos {180^ \circ } = 1$
So we can write it as, we get,
$\Rightarrow {1^{{i}}} = {4^{{i}}}$
Here ${1^{{i}}} = 1$we get,
$\Rightarrow 1 = {4^{{i}}}$
We get,
$\Rightarrow {{i = 0}}$

Hence the correct option is $\left( {{A}} \right)$.

Note: We can get the same value for i if we even consider another two conditions. We can do another method for the same question which gives the same value for$i$.
Net gravitational force is equal to zero.
All Diagonal opposite vertices should have equal mass.
${2^i}M{{ }}cos{{ }}60^\circ = {4^i}M{{ }}cos\left( {60^\circ + 180^\circ } \right)\;$
So,$\;I = 0$.