Question

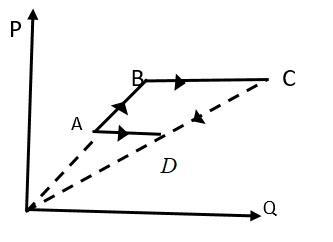
Six moles of an ideal gas performs a cycle shown in figure. The temperatures are ${T_A} = 600K,{T_B} = 800K,{T_C} = 2200K$and${T_D} = 1200K$. The work done by the cycle $ABCDA$ is
A $20KJ$ B$30KJ$ C$40KJ$ D$60KJ$

Answer 1

As we know that we have to find out total work done by the cycle$ABCDA$ , to calculate this we need to find work done by $AB,BC,CD$and$DA$. Then add all of them, and we will get work done by cycle.
Formula used: $\Delta {W_{BC}} = nR\Delta T$
Given: Moles of gas, $n = 6$and Temperatures as below:
${T_A} = 600K$
${T_B} = 800K$
${T_C} = 2200K$
${T_D} = 1200K$

Complete step by step solution:
When volume of a gas remains constant this is known as an isochoric process which is shown by AB and CD given in figure.
$AB$is isochoric process,
So, work done in $AB$will be zero
$\Delta {W_{BC}} = 0......(1)$
When pressure of a gas remains constant then the process will be an isobaric process as shown by BC and DA in the given figure.
$BC$ is isobaric process,
So, work done for ideal gas in $BC$will be
$\Delta {W_{BC}} = nR\Delta T$ (Here R is universal gas constant)
$= nR({T_C} - {T_B})$
Putting values of${T_c}$ , ${T_B}$ and $n$
$= 6 \times R(2200 - 800)$
$= 8400R$
Here we will put value of universal gas constant, $R = 8.3J/K - mol$
$= 8400 \times 8.3 = 69720J......\left( 2 \right)$
$CD$is isochoric process,
So, work done in $CD$will be zero
$\Delta {W_{CD}} = 0......(3)$
$DA$ is isobaric process,
So, work done for ideal gas in $DC$will be
$\Delta {W_{DA}} = nR\Delta T$
$= nR({T_A} - {T_D})$
Putting values of ${T_c}$ , ${T_B}$ and $n$
$= 6 \times R(600 - 1200)$
$= 6 \times R \times \left( { - 600} \right)$
$= - 3600R$
Here we will put value of universal gas constant, $R = 8.3J/K - mol$
$= - 3600 \times 8.3$
$= - 29880J......(4)$
Now, we will add all four work done to find total work done by the cycle$ABCDA$
$\Delta {W_{Total}} = \Delta {W_{AB}} + \Delta {W_{BC}} + \Delta {W_{CD}} + \Delta {W_{DA}}......(5)$
$= 0 + 69720 + 0 - 29880$(Putting values of equation 1, 2, 3 and 4 in equation 5)
$= 39840J$

Here, the total work done by cycle$ABCDA$.

Note: We should note that, to find out work done by a cycle, we must break that cycle in individual parts. And calculate their individual work done with the help of the formula of work done, then add all of them.