Question

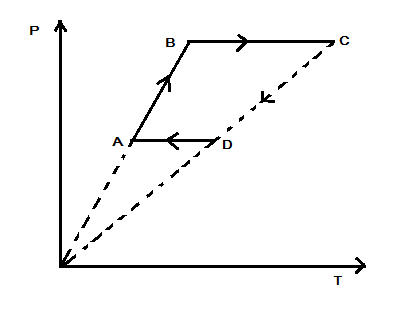
Six moles of an ideal gas performs a cycle shown in figure. The temperatures are ${{T}_{A}}=600K$ , ${{T}_{B}}=800K$ , ${{T}_{C}}=2200K$ and ${{T}_{D}}=1200K$ . The work done by the cycle ABCDA is

(A) 20 kJ
(B) 30 kJ
(C) 40 kJ
(D) 60kJ

Answer 1

Hint : Here, we will have to find the work done for the processes AB, BC, CD and DA to find the work done for the whole cycle. Here, the processes AB and CD are isochoric processes while the processes BC and AD are isobaric, as there is constant pressure. So we apply the work done for these processes and obtain the answer.

Complete Step By Step Answer:
Here, the temperatures at the point A is ${{T}_{A}}=600K$ , at point B is ${{T}_{B}}=800K$ , at point C is ${{T}_{C}}=2200K$ and at point D is ${{T}_{D}}=1200K$ . For the process of AB, the pressure and temperature are changing but the volume is constant. Hence it is an isochoric process and thus the work done would be zero. Thus, we have ${{W}_{(AB)}}=0$ . For the process BC, there is constant pressure, and so the work done is given by the following formula:
${{W}_{(BC)}}=nR\Delta T$
Here, WBC is the work done for process BC, n is the number of moles, R is the ideal gas constant and $\Delta T$ is the change in temperature. Thus, we have;
${{W}_{(BC)}}=6\times R\times 1400 \\\$
$\therefore {{W}_{(BC)}}=8400R \\\$
For the process CD, the process is isochoric so again the work done is zero. Thus, we have ${{W}_{(CD)}}=0$ .
Now, for the process DA, the process is isobaric and hence the work done ${{W}_{(DA)}}=nR\Delta T$ and hence we have the work done as follows:
{W_{(DA)}} = - 6 \times R \times 600 \\\
$\therefore {W_{(DA)}} = - 3600R \\\$
Here, the negative sign is because the cycle is moving in the opposite direction. So we have total work done as:
W = {W_{(BC)}} + {W_{(DA)}} \\\
\Rightarrow W = 8400R - 3600R \\\
\Rightarrow W = 5600 \times 8.3 \\\
$\therefore W = 40kJ \\\$

Note :
The work done in an isochoric process is zero because the volume of the system does not decrease or increase, which is why the system is not doing work as well there is no work done on the system. Also, when there is an isobaric process, the temperature changes and the work done is due to the internal energy of the system.