Question

Six identical uniform rods PQ,QR,RS,ST,TU and UP each weighing W are freely joined at their ends to form a hexagon. The rod PQ is fixed in a horizontal position and the middle points of PQ and ST are connected by a vertical string. The tension in the string is:

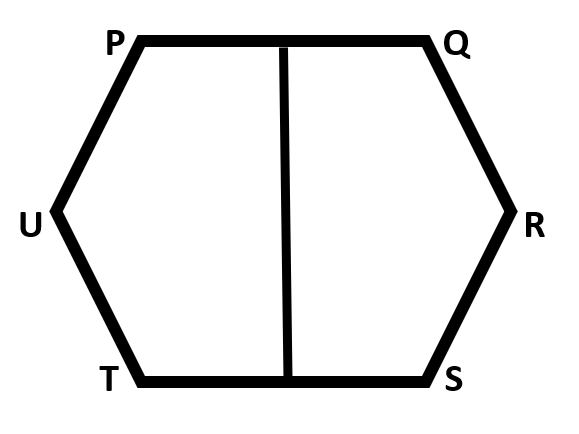
(A) W
(B) 3W
(C) 2W
(D) 4W

Answer 1

In order to find out the net tension in the string, we shall use the concept of virtual work done. This is done by assuming that one part of the system undergoes certain displacement. Then, we shall find the displacements of all the other components in the system in terms of our assumed displacement. Then, since the net work done is zero, we shall equate the sum of all the work done by all the forces as zero.

Complete step by step answer:
: Let the system be given a small displacement ‘y’ in the vertical direction. And we will assume that the rod PQ is our reference line, that is, vertical displacement of rod PQ is equal to zero.
Now, the displacement of the center of rods PU and QR will be ‘y’. Since, the rods PU and QR are stretched downwards, they will push the rods beneath them thus, the rods UT and RS will also stretch down by the same amount, that is, ‘y’.
Now, for the rod TS, the net stretch is equal to the sum of displacements of the rods at two sides taken individually, that is, equal to ‘2y’.
And, therefore the net stretch in the string is also equal to ‘2y’ as it is connected to PQ and TS. Thus, applying the virtual work theorem in the above system, we get:
$\Rightarrow W(y)+W(y)+W(y)+W(y)+W(2y)=T(2y)$
Where, ‘T’ is the tension in the string. Simplifying the above equation, we get:
$\begin{aligned} & \Rightarrow 6Wy=2Ty \\\ & \therefore T=3W \\\ \end{aligned}$
Hence, the tension in the string comes out to be 3W.

So, the correct answer is “Option B”.

Note: In problems like these, if no data is provided we should work the problem under certain assumptions and try to get our solution. Also, the concept of virtual work is a very helpful concept. Apart from questions like these, it is used in calculating the relation between tensions in complex pulley-system problems.