Question

Sirius has a parallax of 0.377 arc seconds. How far is it away?

Answer 1

Hint : We will be using the theory of parallax. We will also use the relation between the parallax angle and the distance of the object.
Formula to calculate the distance of the object using its parallax angle.
Distance $d=\dfrac{1}{p}$
Where $p$ is the parallax angle.

Complete Step By Step Answer:
As we know, the term parallax refers to the semi-angle of inclination between two lines of sight to the star, as observed when earth is on opposite sides of the sun in its orbit.

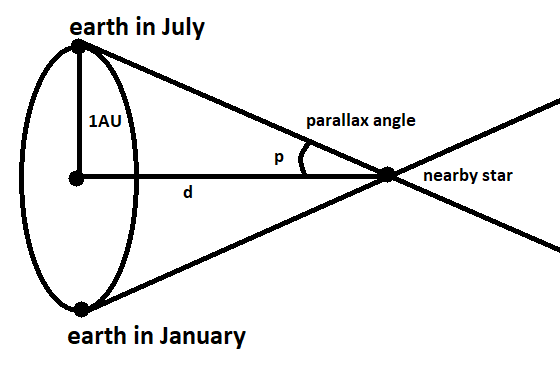
Now as we can see from the figure that the parallax angle depends upon the distance of the star from the center of the earth. Therefore, we can say that the farther away the star is, the smaller will be the parallax angle and vice versa.
Now, as we look at the data given in the question,
The parallax angle is given to be $p=0.377\;arcseconds$
We also know that the distance between the sun and the earth is $R=1AU$ (Astronomy)
Also, we can conclude that the distance of the star is very large than$R$ , the distance of the star from the earth and the sun can be considered the same i.e.,$d$
We know the radius of the earth and the parallax angle. Therefore using a trigonometric identity we can write
$\tan \theta =\dfrac{R}{d}$
$\Rightarrow d=\dfrac{R}{\tan \theta }$
There is one thing to note now that the parallax angle is so small that we can write $\tan \theta =\theta$
$\begin{aligned} & \Rightarrow d=\dfrac{R}{\theta } \\\ & \Rightarrow d=\dfrac{1}{0.377} \\\ & \Rightarrow d=2.652par\sec \\\ & \Rightarrow d=8.64lightyears \\\ \end{aligned}$
Therefore, we found that the distance of the star is $8.64lightyears$

Note :
We must always remember to see the units in which the data is given. Mostly, the distance of the star is measured in $parsec$ and the angle of parallax in$arcseconds$ . If the distance is given and you have to find the parallax angle, then first of all convert the distance into $par\sec$ if it is given in$lightyears$ .