Question

From a circular disk of radius R, a triangular portion is cut (see figure). The distance of the o of mass of the remainder from the centre of the disk is-

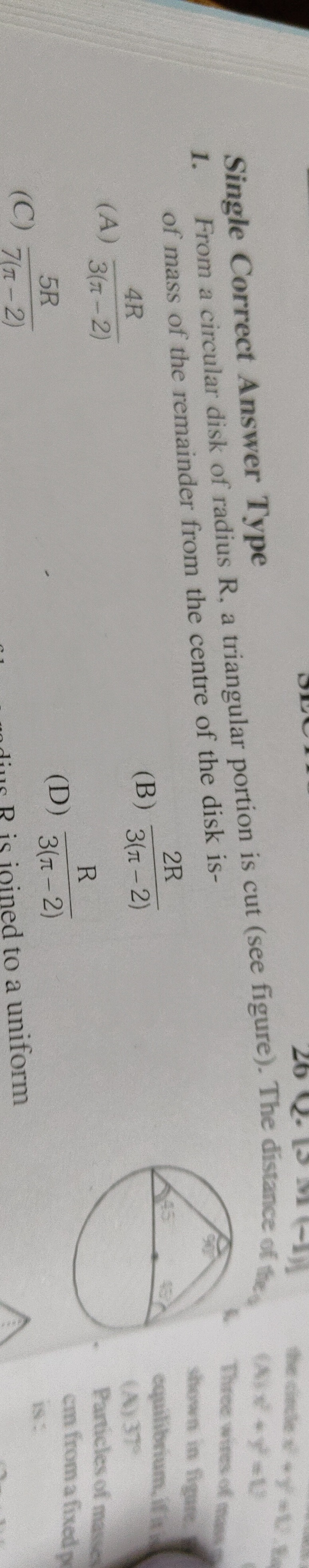
• A. $\frac{4R}{3(\pi-2)}$
• B. $\frac{2R}{3(\pi -2)}$
• C. $\frac{5R}{7(\pi−2)}$
• D. $\frac{R}{3(\pi -2)}$

Answer 1

Answer: (B)

$\frac{2R}{3(\pi -2)}$

Answer 2

The problem is solved by considering the center of mass of the original disk, the cut-out triangle, and the remaining portion. By assuming the area of the cut portion is $2R^2$ (instead of the $R^2/2$ suggested by the diagram) and the center of mass of this cut portion is at a distance $R/3$ from the center, we can arrive at the correct answer using the principle of superposition for center of mass.