Question

The equation $Sinfx=8\sqrt{x+T}$ is given. Interpret 'Sinfx' as 'x' and solve for $x$ in terms of $T$. Consider the conditions for real solutions.

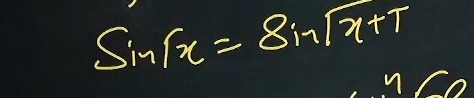
Answer 1

If $T < -16$, no real solutions. If $T = -16$, $x = 32$. If $-16 < T \le 0$, $x = 32 + 8\sqrt{16+T}$ and $x = 32 - 8\sqrt{16+T}$. If $T > 0$, $x = 32 + 8\sqrt{16+T}$.

Answer 2

The original equation is interpreted as $x = 8\sqrt{x+T}$. For the square root to be defined, $x+T \ge 0$. Also, since $8\sqrt{x+T} \ge 0$, we must have $x \ge 0$. Squaring both sides gives $x^2 = 64(x+T)$, which rearranges to the quadratic equation $x^2 - 64x - 64T = 0$. Using the quadratic formula, $x = \frac{64 \pm \sqrt{(-64)^2 - 4(1)(-64T)}}{2} = \frac{64 \pm \sqrt{4096 + 256T}}{2} = \frac{64 \pm 16\sqrt{16+T}}{2} = 32 \pm 8\sqrt{16+T}$.

We must check the validity of these solutions against the conditions $x \ge 0$ and $x+T \ge 0$.

1. Real solutions: For $\sqrt{16+T}$ to be real, $16+T \ge 0 \implies T \ge -16$.
2. Condition $x \ge 0$:
   • $x_1 = 32 + 8\sqrt{16+T}$. Since $\sqrt{16+T} \ge 0$ for $T \ge -16$, $x_1 \ge 32$, so $x_1 \ge 0$ is always satisfied.
   • $x_2 = 32 - 8\sqrt{16+T}$. For $x_2 \ge 0$, we need $32 \ge 8\sqrt{16+T} \implies 4 \ge \sqrt{16+T}$. Squaring both sides (which are non-negative), $16 \ge 16+T \implies T \le 0$.
3. Condition $x+T \ge 0$: This condition is generally satisfied if $x \ge 0$ for the solutions derived from squaring, except possibly when $x=0$ and $T=0$. If $x=0$, then $0 = 8\sqrt{T}$, implying $T=0$. In this case, $x+T=0 \ge 0$.

Combining these conditions:

• If $T < -16$: No real solutions as $\sqrt{16+T}$ is not real.
• If $T = -16$: $x = 32 \pm 8\sqrt{0} = 32$. This solution is valid ($32 \ge 0$ and $32-16 = 16 \ge 0$).
• If $-16 < T < 0$: Both $x_1 = 32 + 8\sqrt{16+T}$ and $x_2 = 32 - 8\sqrt{16+T}$ are valid because $T \ge -16$ and $T \le 0$ are met.
• If $T = 0$: $x = 32 \pm 8\sqrt{16} = 32 \pm 32$, so $x=64$ or $x=0$. Both are valid. Note that $x_2 = 32 - 8\sqrt{16} = 0$, which satisfies $T \le 0$.
• If $T > 0$: $T \ge -16$ is met, but $T \le 0$ is not met for $x_2$. Thus, only $x_1 = 32 + 8\sqrt{16+T}$ is a valid solution.

The complete solution set is:

• If $T < -16$: No real solutions.
• If $T = -16$: $x = 32$.
• If $-16 < T \le 0$: $x = 32 + 8\sqrt{16+T}$ and $x = 32 - 8\sqrt{16+T}$.
• If $T > 0$: $x = 32 + 8\sqrt{16+T}$.