Question
Question: $\sin(\frac{2\pi}{7})+\sin(\frac{4\pi}{7})+\sin(\frac{8\pi}{7})$...
sin(72π)+sin(74π)+sin(78π)
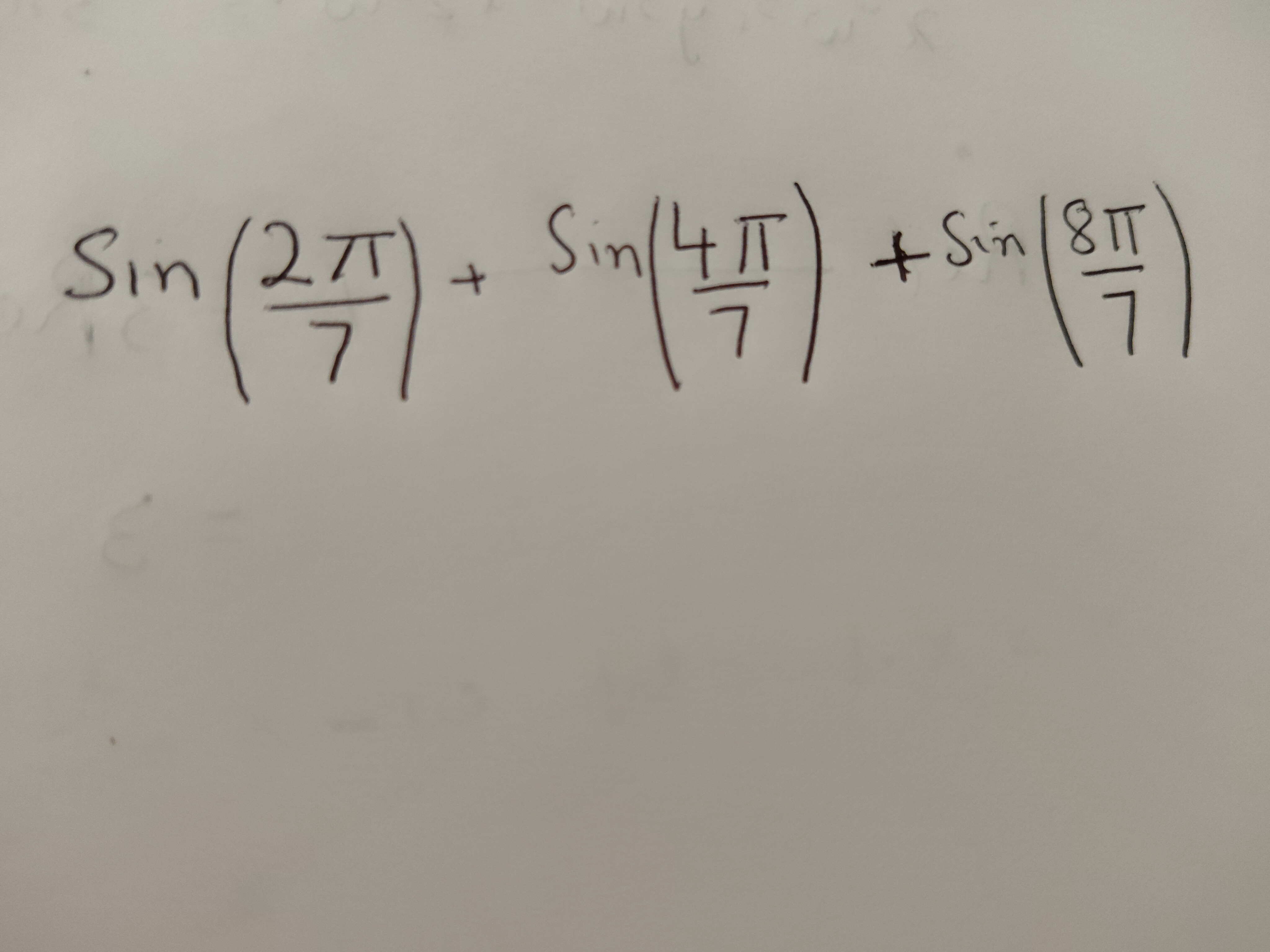
27
Solution
The problem asks to evaluate the sum S=sin(72π)+sin(74π)+sin(78π).
First, let's simplify the term sin(78π): sin(78π)=sin(π+7π)=−sin(7π).
So the sum becomes: S=sin(72π)+sin(74π)−sin(7π).
This is a common problem that can be solved using properties of complex numbers and roots of unity, specifically Gaussian periods. Let ω=ei72π. The roots of z7−1=0 are ωk for k=0,1,…,6. The sum of all roots is zero: ∑k=06ωk=1+ω+ω2+ω3+ω4+ω5+ω6=0.
Let's consider the quadratic residues modulo 7. The non-zero residues are {1,2,3,4,5,6}. The quadratic residues are 12≡1, 22≡4, 32≡9≡2. So, the set of quadratic residues is R={1,2,4}. The set of quadratic non-residues is N={3,5,6}.
Define the Gaussian periods: η0=∑k∈Rωk=ω1+ω2+ω4=ei72π+ei74π+ei78π. η1=∑k∈Nωk=ω3+ω5+ω6=ei76π+ei710π+ei712π.
From the sum of all roots: 1+η0+η1=0⟹η0+η1=−1.
Now, let's consider the product η0η1: η0η1=(ω1+ω2+ω4)(ω3+ω5+ω6) =ω4+ω6+ω7+ω5+ω7+ω8+ω7+ω9+ω10. Since ω7=1, we have: η0η1=ω4+ω6+1+ω5+1+ω1+1+ω2+ω3 (using ω8=ω, ω9=ω2, ω10=ω3) Rearranging the terms: η0η1=3+(ω1+ω2+ω3+ω4+ω5+ω6). Since ∑k=16ωk=−1: η0η1=3+(−1)=2.
So we have a system of equations for η0 and η1:
- η0+η1=−1
- η0η1=2
η0 and η1 are the roots of the quadratic equation x2−(η0+η1)x+η0η1=0: x2−(−1)x+2=0⟹x2+x+2=0. Using the quadratic formula, x=2(1)−1±12−4(1)(2)=2−1±1−8=2−1±−7=2−1±i7.
So, {η0,η1}={2−1+i7,2−1−i7}. We need to determine which one is η0. η0=cos(72π)+cos(74π)+cos(78π)+i(sin(72π)+sin(74π)+sin(78π)). The sum we want to evaluate is the imaginary part of η0.
Let's analyze the real part of η0: Re(η0)=cos(72π)+cos(74π)+cos(78π). We know cos(78π)=cos(2π−76π)=cos(76π). So, Re(η0)=cos(72π)+cos(74π)+cos(76π). We know that cos(72π)>0, cos(74π)<0, cos(76π)<0. However, the sum cos(72π)+cos(74π)+cos(76π) is negative. Consider the full sum of cosines: ∑k=16cos(72kπ)=cos(72π)+cos(74π)+cos(76π)+cos(78π)+cos(710π)+cos(712π)=−1. Using cos(72kπ)=cos(72(7−k)π), we have: cos(78π)=cos(76π) cos(710π)=cos(74π) cos(712π)=cos(72π) So, 2(cos(72π)+cos(74π)+cos(76π))=−1. Therefore, cos(72π)+cos(74π)+cos(76π)=−21. This means Re(η0)=−21.
Comparing this with the possible values for x: 2−1+i7 has real part −21. 2−1−i7 has real part −21. Both have the same real part.
Now we need to determine the sign of the imaginary part. S=sin(72π)+sin(74π)−sin(7π). We know that for x∈(0,π), sin(x)>0. 72π≈0.897 radians, which is in the first quadrant. sin(72π)>0. 74π≈1.795 radians, which is in the second quadrant. sin(74π)>0. 7π≈0.448 radians, which is in the first quadrant. sin(7π)>0.
We need to compare the magnitudes. Consider the function f(x)=sin(x). It is concave down on (0,π). The angles are 7π,72π,74π. We know sin(74π)=sin(73π). So S=sin(72π)+sin(73π)−sin(7π). Let x=7π. Then S=sin(2x)+sin(3x)−sin(x). S=2sin(x)cos(x)+(3sin(x)−4sin3(x))−sin(x). S=sin(x)(2cos(x)+3−4sin2(x)−1). S=sin(x)(2cos(x)+2−4(1−cos2(x))). S=sin(x)(2cos(x)+2−4+4cos2(x)). S=sin(x)(4cos2(x)+2cos(x)−2). S=2sin(x)(2cos2(x)+cos(x)−1). S=2sin(x)(2cos(x)−1)(cos(x)+1). Since x=7π, which is in the first quadrant, sin(x)>0 and cos(x)>0. Also, cos(x)+1>0. We need to check the sign of (2cos(x)−1). For x=7π, x<3π. Since cos(x) is a decreasing function in (0,π), cos(7π)>cos(3π)=21. So 2cos(7π)>1, which means 2cos(7π)−1>0. Therefore, S>0.
Since Re(η0)=−21 and Im(η0)>0, we must have: η0=2−1+i7.
The value we are looking for is the imaginary part of η0. Im(η0)=27.
