Question
Question: $\sin^6x + \cos^6x = \frac{1}{6}$...
sin6x+cos6x=61
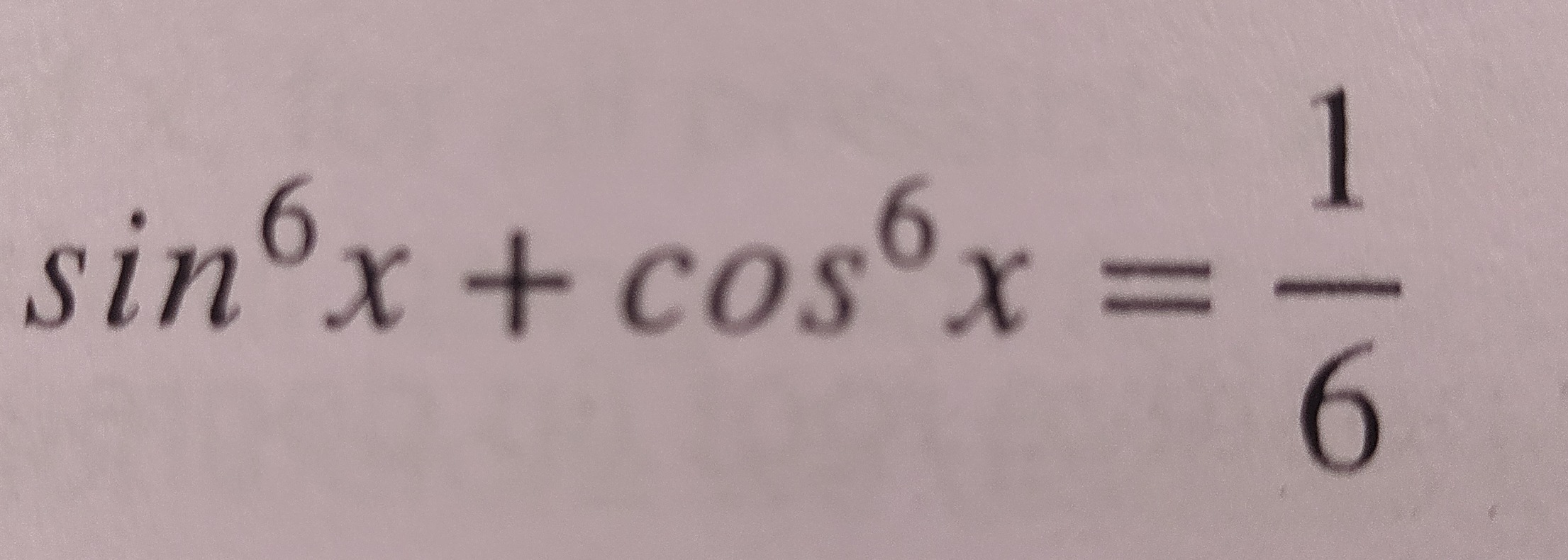
Answer
The equation has no real solutions. The solution set is ∅.
Explanation
Solution
The equation sin6x+cos6x=61 is simplified using the identity sin6x+cos6x=1−3sin2xcos2x.
The equation becomes 1−3sin2xcos2x=61.
Solving for sin2xcos2x gives sin2xcos2x=185.
Using the identity sin2(2x)=4sin2xcos2x, we get sin2(2x)=4⋅185=910.
Since the maximum possible value of sin2(2x) for real x is 1, and 910>1, the equation sin2(2x)=910 has no real solutions.
Thus, the original equation has no real solutions. The solution set is empty.
