Question
Question: $\sin^4x + \cos^4x + \sin2x + \alpha = 0$ Range of $\alpha = ?$...
sin4x+cos4x+sin2x+α=0
Range of α=?
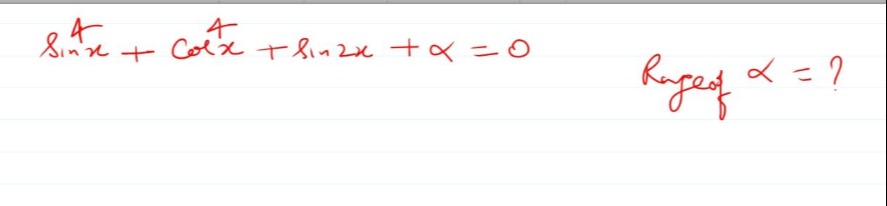
[−23,21]
Solution
To find the range of α for which the equation sin4x+cos4x+sin2x+α=0 has real solutions for x, we first simplify the trigonometric expression.
Step 1: Simplify sin4x+cos4x
We know the identity a2+b2=(a+b)2−2ab. Let a=sin2x and b=cos2x.
sin4x+cos4x=(sin2x+cos2x)2−2sin2xcos2x
Since sin2x+cos2x=1, this simplifies to:
sin4x+cos4x=12−2(sinxcosx)2
We also know that sin2x=2sinxcosx, which means sinxcosx=2sin2x.
Substitute this into the expression:
sin4x+cos4x=1−2(2sin2x)2
sin4x+cos4x=1−24sin22x
sin4x+cos4x=1−2sin22x
Step 2: Substitute the simplified expression back into the original equation
The given equation becomes:
(1−2sin22x)+sin2x+α=0
Step 3: Introduce a substitution
Let y=sin2x. Since x is a real number, sin2x can take any value in its standard range, i.e., y∈[−1,1].
The equation transforms into an algebraic equation in terms of y:
1−2y2+y+α=0
Step 4: Express α in terms of y
Rearrange the equation to isolate α:
α=2y2−y−1
Step 5: Find the range of α by analyzing the function f(y)=2y2−y−1 for y∈[−1,1]
This is a quadratic function f(y)=ay2+by+c with a=1/2, b=−1, and c=−1. Since the coefficient of y2 (a=1/2) is positive, the parabola opens upwards. The vertex of the parabola is located at y=−2ab.
yvertex=−2(1/2)−1=−1−1=1.
The interval for y is [−1,1]. The vertex y=1 is included in this interval and is at its right boundary. For an upward-opening parabola, the minimum value within an interval occurs either at the vertex or at one of the endpoints. Since the vertex is at y=1, this is where the minimum value occurs within the interval [−1,1].
Minimum value of f(y) at y=1:
f(1)=2(1)2−(1)−1=21−1−1=21−2=−23.
The maximum value of f(y) within the interval [−1,1] will occur at the endpoint furthest from the vertex. The vertex is at y=1. The distance from y=1 to y=−1 is ∣1−(−1)∣=2. The distance from y=1 to y=1 is 0. Thus, the maximum value occurs at y=−1.
Maximum value of f(y) at y=−1:
f(−1)=2(−1)2−(−1)−1=21+1−1=21.
Therefore, the range of the function f(y)=2y2−y−1 for y∈[−1,1] is [−23,21]. This is the required range for α.
