Question

$\sin \left( A+B \right)=\sin A\cos B+\cos A\sin B$ . If true then write 1 and if false then write 0.

Answer 1

Hint: For proving the given relation, take a right angle triangle with one angle as A + B. split this angle to A and B by a line. Draw perpendicular by the vertex of the triangle to the line. Solve it further.
$\sin \theta =\dfrac{\text{Perpendicular}}{\text{Hypotenuse}},cos\theta =\dfrac{\text{Base}}{\text{Hypotenuse}}$

Complete step-by-step answer:
Given in the question is
$\sin \left( A+B \right)=\sin A\cos B+\cos A\sin B....................\left( i \right)$
Let us suppose a right angle with one angle of it as (A + B).

Let us split angle A + B into two angles i.e. A and B. Diagram can be given as

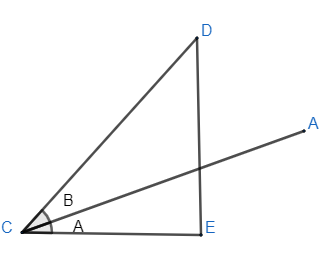
Now, draw a perpendicular to the line AC meeting at F and draw a perpendicular from point F to side ED. So we get diagram as

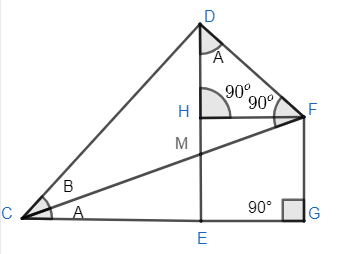
Where FG is perpendicular to line CE. Now, CE and HF are two lines that are perpendicular to the same line DE. It means CE and HF should be parallel to each because perpendicular to any line will have only one direction. So, $HF||CE$.
Hence, $\angle HFM=A$ because of corresponding angles formed by a transversal with two parallel lines. As we know, the sum of all angles of a triangle is ${{180}^{\circ }}$.
So, in $\Delta FHM$
$\begin{aligned} & \angle HFM+\angle FMH+\angle MHF={{180}^{\circ }} \\\ & A+\angle FMH+90={{180}^{\circ }} \\\ & \angle FMH=90-A............................\left( i \right) \\\ \end{aligned}$
Now, in $\Delta DFM$ , we get
$\angle DFM+\angle FMD+\angle MDF={{180}^{\circ }}$
Using equation (i) we get

& {{90}^{\circ }}+{{90}^{\circ }}-A+\angle MDF={{180}^{\circ }} \\\ & \angle MDF=A....................\left( ii \right) \\\ \end{aligned}$$ Now, take $\sin C,\sin \left( A+B \right)$ in $\Delta DCE$ we get $\begin{aligned} & \sin \left( A+B \right)=\dfrac{\text{Perpendicular}}{\text{Hypotaneous}}.....................\left( iii \right) \\\ & \sin \left( A+B \right)=\dfrac{DE}{CD}..............................\left( iv \right) \\\ \end{aligned}$ Now, we can write DE as sum of length DH and HE, we get DE = DH + HE……………………(v) So, we get from equation (iv) and (v) as $\begin{aligned} & \sin \left( A+B \right)=\dfrac{DH+HE}{CD} \\\ & Sin\left( A+B \right)=\dfrac{DH}{CD}+\dfrac{HE}{CD} \\\ \end{aligned}$ Now, multiply and divide the first fraction on RHS by FD and second fraction by CF. So we get value of $\sin \left( A+B \right)$ as $\begin{aligned} & \sin \left( A+B \right)=\dfrac{DH}{CD}\times \dfrac{FD}{FD}+\dfrac{HE}{CD}\times \dfrac{CF}{CF} \\\ & \sin \left( A+B \right)=\dfrac{DH}{FD}\times \dfrac{FD}{CD}+\dfrac{HE}{CF}\times \dfrac{CF}{CD}.........................\left( vi \right) \\\ \end{aligned}$ Now from $\Delta DFC$ we get $\sin B=\dfrac{FD}{CD},\cos B=\dfrac{CF}{CD}$ And from $\Delta DHF$ we get $\cos A=\dfrac{DH}{FD}$ Similarly, from $\Delta CFG$ we get $\sin A=\dfrac{FG}{CF}$ As FG = HE, because HFGE is acting as a rectangle, all the angles of HFGE are ${{90}^{\circ }}$ . So, we can write the value of $\sin A$ as $\sin A=\dfrac{HE}{CF}$ Now, we can use above relation with the equation (vi) and hence we get $\begin{aligned} & \sin \left( A+B \right)=\cos A\sin B+\sin A\cos B, \\\ & \sin \left( A+B \right)=\sin A\cos B+\cos A\sin B \\\ \end{aligned}$ Hence, the given relation is proved. So, the given expression in the problem is true. So, the answer should be 1 as the statement is true. Note: One may verify the equation by putting some values of A and B. Example: $A={{30}^{\circ }},B={{60}^{\circ }}$. So, it can be another approach for these kinds of questions. Constructing the diagram mentioned in the solution is the key point for proving the given relation. One may prove the relation of $\tan \left( A+B \right),\sin \left( A-B \right),\cos \left( A+B \right)$. As well with the same approach.