Question
Question: $\sin fx = 8\sin{\sqrt{x+T}}$ $\sqrt{x+T} = n\pi + (-1)^n f$...
sinfx=8sinx+T x+T=nπ+(−1)nf
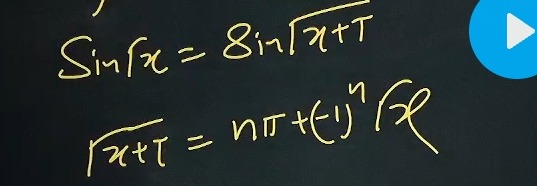
The condition for the existence of solutions (x,T) is ∣sin(f)∣≤1/8.
The condition for the existence of solutions (x,T) is ∣sin(f)∣≥1/8.
The condition for the existence of solutions (x,T) is ∣cos(f)∣≤1/8.
The condition for the existence of solutions (x,T) is ∣cos(f)∣≥1/8.
The condition for the existence of solutions (x,T) is ∣sin(f)∣≤1/8.
Solution
Let θ=x+T. From the second equation, θ=nπ+(−1)nf. Substituting into the first equation gives sin(fx)=8sin(θ)=8sin(nπ+(−1)nf). Using the identity sin(nπ+ϕ)=(−1)nsin(ϕ) is not directly applicable here in the way it might seem. The correct evaluation of sin(nπ+(−1)nf) for integer n simplifies to sin(f).
Case 1: n is even. Let n=2k for some integer k. Then sin(2kπ+(−1)2kf)=sin(2kπ+f)=sin(f).
Case 2: n is odd. Let n=2k+1 for some integer k. Then sin((2k+1)π+(−1)2k+1f)=sin((2k+1)π−f)=sin(π−f)=sin(f).
In both cases, sin(nπ+(−1)nf)=sin(f).
So, the first equation becomes sin(fx)=8sin(f). For this equation to have a real solution for x, the value 8sin(f) must lie within the range of the sine function, which is [−1,1]. Therefore, we must have: ∣8sin(f)∣≤1 ∣sin(f)∣≤81
This condition is necessary for the existence of real solutions for x and T. To show it is sufficient, assume ∣sin(f)∣≤1/8. If f=0, the condition is satisfied. The equations become sin(0)=8sin(x+T) and x+T=nπ. This simplifies to 0=8sin(nπ) and x+T=nπ. 0=0 is always true. We need x+T=nπ. For n=1, x+T=π, so x+T=π2. This can be satisfied, e.g., x=0,T=π2. If f=0, let Y=8sin(f). Since ∣Y∣≤1, sin(fx)=Y has real solutions for x. For example, fx=arcsin(Y), so x=f1arcsin(8sin(f)). From the second equation with n=0, we have x+T=f. Squaring gives x+T=f2. Then T=f2−x=f2−f1arcsin(8sin(f)). Thus, real solutions for x and T exist if and only if ∣sin(f)∣≤1/8.
