Question
Question: Simplify: $(\sqrt{2}+1)^{6}-(\sqrt{2}-1)^{6}$...
Simplify: (2+1)6−(2−1)6
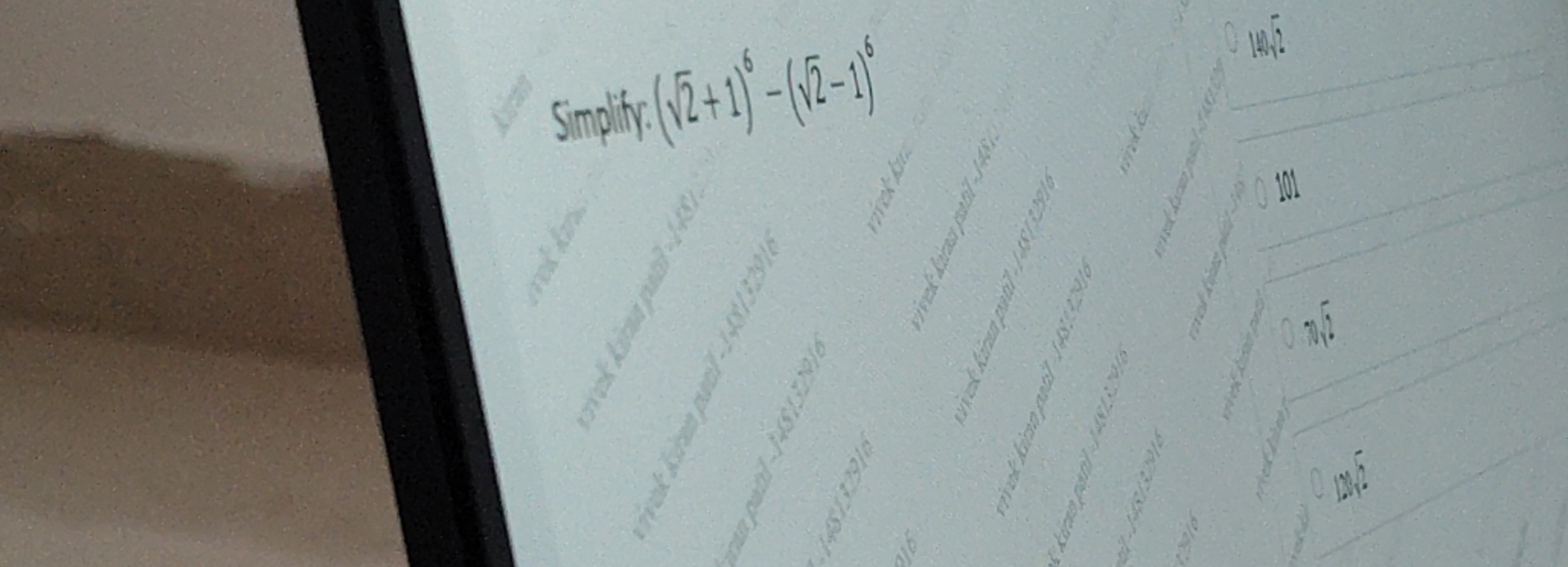
1402
101
702
1202
1402
Solution
To simplify the expression (2+1)6−(2−1)6, we can use the binomial theorem.
Let a=2 and b=1. The expression is of the form (a+b)6−(a−b)6.
The binomial expansion for (a+b)n is: (a+b)n=(0n)anb0+(1n)an−1b1+(2n)an−2b2+⋯+(nn)a0bn
The binomial expansion for (a−b)n is: (a−b)n=(0n)anb0−(1n)an−1b1+(2n)an−2b2−⋯+(−1)n(nn)a0bn
When we subtract (a−b)n from (a+b)n, the terms with even powers of b cancel out, and the terms with odd powers of b are doubled: (a+b)n−(a−b)n=2[(1n)an−1b1+(3n)an−3b3+(5n)an−5b5+…]
In this case, n=6, a=2, and b=1. So, the expression becomes: (2+1)6−(2−1)6=2[(16)(2)6−1(1)1+(36)(2)6−3(1)3+(56)(2)6−5(1)5] =2[(16)(2)5+(36)(2)3+(56)(2)1]
Now, we calculate the binomial coefficients and powers of 2: (16)=6 (36)=3×2×16×5×4=20 (56)=(6−56)=(16)=6
(2)1=2 (2)3=(2)2×2=22 (2)5=(2)4×2=((2)2)2×2=22×2=42
Substitute these values back into the expression: =2[6(42)+20(22)+6(2)] =2[242+402+62] =2[(24+40+6)2] =2[702] =1402
