Solveeit Logo
Login

Question

Question: Simplify: \[\dfrac{{{{\sin }^3}\theta + {{\cos }^3}\theta }}{{\sin \theta + \cos \theta }} + \sin...

Simplify:
sin⁡3θ+cos⁡3θsin⁡θ+cos⁡θ+sin⁡θcos⁡θ\dfrac{{{{\sin }^3}\theta + {{\cos }^3}\theta }}{{\sin \theta + \cos \theta }} + \sin \theta \cos \theta

Explanation

Solution

Here we will use the formula of (a3+b3)=(a+b)(a2+b2−ab)\left( {{a^3} + {b^3}} \right) = \left( {a + b} \right)\left( {{a^2} + {b^2} - ab} \right), aa and bb are two different values. We will simplify using this formula to simplify the given trigonometric equation.

Complete step-by-step solution:
Step 1: By comparing the given term sin⁡3θ+cos⁡3θ{\sin ^3}\theta + {\cos ^3}\theta with the formula (a3+b3)=(a+b)(a2+b2−ab)\left( {{a^3} + {b^3}} \right) = \left( {a + b} \right)\left( {{a^2} + {b^2} - ab} \right), we can write it as below:
⇒(sin⁡3θ+cos⁡3θ)=(sin⁡θ+cos⁡θ)(sin⁡2θ+cos⁡2θ−sin⁡θcos⁡θ)\Rightarrow \left( {{{\sin }^3}\theta + {{\cos }^3}\theta } \right) = \left( {\sin \theta + \cos \theta } \right)\left( {{{\sin }^2}\theta + {{\cos }^2}\theta - \sin \theta \cos \theta } \right)
By substituting this value in this given expression sin⁡3θ+cos⁡3θsin⁡θ+cos⁡θ+sin⁡θcos⁡θ\dfrac{{{{\sin }^3}\theta + {{\cos }^3}\theta }}{{\sin \theta + \cos \theta }} + \sin \theta \cos \theta , we get:
⇒(sin⁡θ+cos⁡θ)(sin⁡2θ+cos⁡2θ−sin⁡θcos⁡θ)sin⁡θ+cos⁡θ+sin⁡θcos⁡θ\Rightarrow \dfrac{{\left( {\sin \theta + \cos \theta } \right)\left( {{{\sin }^2}\theta + {{\cos }^2}\theta - \sin \theta \cos \theta } \right)}}{{\sin \theta + \cos \theta }} + \sin \theta \cos \theta ……………………… (1)
Step 2: By dividing the term sin⁡θ+cos⁡θ\sin \theta + \cos \theta from the numerator and denominator side, we get:
⇒(sin⁡2θ+cos⁡2θ−sin⁡θcos⁡θ)+sin⁡θcos⁡θ\Rightarrow \left( {{{\sin }^2}\theta + {{\cos }^2}\theta - \sin \theta \cos \theta } \right) + \sin \theta \cos \theta
By eliminating the term sin⁡θcos⁡θ\sin \theta \cos \theta from the above expression (sin⁡2θ+cos⁡2θ−sin⁡θcos⁡θ)+sin⁡θcos⁡θ\left( {{{\sin }^2}\theta + {{\cos }^2}\theta - \sin \theta \cos \theta } \right) + \sin \theta \cos \theta , we get:
⇒sin⁡2θ+cos⁡2θ\Rightarrow {\sin ^2}\theta + {\cos ^2}\theta
Step 3: As we know the value of sin⁡2θ+cos⁡2θ=1{\sin ^2}\theta + {\cos ^2}\theta = 1, so the answer will be equal to 11.

∴sin⁡3θ+cos⁡3θsin⁡θ+cos⁡θ+sin⁡θcos⁡θ=1\therefore \dfrac{{{{\sin }^3}\theta + {{\cos }^3}\theta }}{{\sin \theta + \cos \theta }} + \sin \theta \cos \theta = 1

Note: Students need to remember the basic formulas for solving these types of questions. Some of them are mentioned below:
(a+b)2=(a2+b2+2ab){\left( {a + b} \right)^2} = \left( {{a^2} + {b^2} + 2ab} \right)
(a−b)2=(a2+b2−2ab){\left( {a - b} \right)^2} = \left( {{a^2} + {b^2} - 2ab} \right)
(a+b)3=a3+b3+3ab(a+b){\left( {a + b} \right)^3} = {a^3} + {b^3} + 3ab\left( {a + b} \right)
(a−b)3=a3−b3−3ab(a−b){\left( {a - b} \right)^3} = {a^3} - {b^3} - 3ab\left( {a - b} \right)
(a3+b3)=(a+b)(a2+b2−ab)\left( {{a^3} + {b^3}} \right) = \left( {a + b} \right)\left( {{a^2} + {b^2} - ab} \right)
(a3+b3)=(a−b)(a2+b2+ab)\left( {{a^3} + {b^3}} \right) = \left( {a - b} \right)\left( {{a^2} + {b^2} + ab} \right)
Also, students need to remember that the value of sin⁡2θ+cos⁡2θ=1{\sin ^2}\theta + {\cos ^2}\theta = 1 , proof of which as shown below for your better understanding:
Assume that in a triangle, there are three sides of length xx, yyand zz as shown in the below figure:

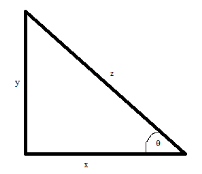
As we know
sin⁡θ=yz\sin \theta = \dfrac{y}{z} , i.e. the Opposite side is divided by the hypotenuses. And the cos⁡θ=xz\cos \theta = \dfrac{x}{z}, i.e. base divided by the hypotenuses.
By using the Pythagoras theorem, we get:
z2=x2+y2{z^2} = {x^2} + {y^2} i.e. (Hypotenuse)2=(Base)2+(height)2{\left( {{\text{Hypotenuse}}} \right)^2} = {\left( {{\text{Base}}} \right)^2} + {\left( {{\text{height}}} \right)^2}
Also,
sin⁡2θ+cos⁡2θ=(yz)2+(xz)2{\sin ^2}\theta + {\cos ^2}\theta = {\left( {\dfrac{y}{z}} \right)^2} + {\left( {\dfrac{x}{z}} \right)^2}, by taking zz common from the denominator part and adding the numerator one we get: