Question

Sides AB and BE of a right triangle, right angled at B are of lengths 16 cm and 8 cm respectively. The length of the side of largest square FDGB that can be inscribed in the triangle ABE is

Answer 1

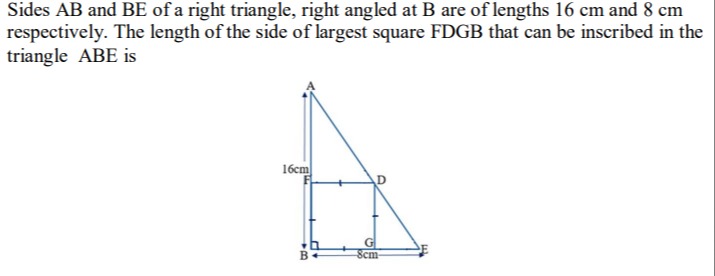
16/3

Answer 2

Place the triangle in the coordinate plane with
  B = (0, 0),
  A = (16, 0) (since AB = 16 cm), and
  E = (0, 8) (since BE = 8 cm).

Assume the square has side length s with one vertex at B. Let   F = (s, 0) (on side AB),   G = (0, s) (on side BE), and   D = (s, s).

The vertex D must lie on the hypotenuse AE. The line AE passes through A (16, 0) and E (0, 8). Its equation is found as follows:   Slope, m = (8 – 0)⁄(0 – 16) = –½.   Using point A:  y = –½(x – 16) ⇒  y = –½x + 8.

Substitute D = (s, s) into the line equation:   s = –½·s + 8 ⟹ s + ½s = 8 ⟹ (3⁄2)s = 8 ⟹ s = (8 × 2)⁄3 = 16⁄3.