Question

Shown in the figure is a shell made of a conductor. It has inner radius $a$ and outer radius $b$, and carries charge $Q$. At its centre is a dipole $\vec P$ as shown, in this case:

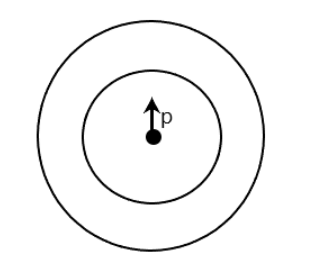
(A) Electric field outside the shell is the same as that of a point charge at the centre of the shell
(B) Surface charge density on the inner surface of shell is zero everywhere
(C) Surface charge density on the inner surface $Q/2$ is uniform and equal to $E = \dfrac{{Q/2}}{{4\pi {a^2}}}$
(D) Surface charge density on the outer surface depends on $\left| {\vec P} \right|$

Answer 1

Due to the presence of the dipole, charge density inside the shell will at some point exist. Since it is a dipole, the charge induced on the outer shell will be equal to zero.
Formula used: In this solution we will be using the following formulae;
$E = K\dfrac{Q}{{{r^2}}}$ where $E$ is the electric field of a charge distribution of total charge $Q$ with distance greater than radius, and $r$ is the distance of interest from the centre. $K$ is a constant.

Complete Step-by-Step Solution:
We have a shell made of a conductor. It has an inner radius of a particular length, and an outer radius of a particular length. There’s a dipole $\vec P$ at the centre but the shell in general has a charge Q. We are to identify which of the statements will hold true.
Let’s investigate what happens to the shell due to the presence of the dipole, basically the electrostatic state of the shell.
Now, as it is known, a dipole is an equal and negative charge separated by a distance. Let’s assume first that the shell is uncharged. The positive side of the dipole will induce a negative charge on the inner shell closest to it, and the negative side of the dipole will induce a positive charge on the other side.
However, because the dipole has a total charge of zero, the charge induced on the outer surface is hence zero. Observe that for the uncharged sphere the total charge is hence zero so the electric field outside is zero. However the shell is actually charged with a charge $Q$. The electric field due to a charge distribution of a charge at the surface is given as
$E = K\dfrac{Q}{{{r^2}}}$, hence this is like a charge at the centre of the shell.

Thus, the correct option is A.

Note: For clarity, the charge induced on the outside is zero because, while the charge induced on the inner is held by the dipole tending to leave its opposite charge behind. However, the shell is conducting, hence the positive negative will recombine allowing the induction to cancel.