Question
Question: Show that voltage leads current by \[\dfrac{\pi }{2}\], when A.C. voltage applied to pure inductanc...
Show that voltage leads current by 2π, when A.C. voltage applied to pure inductance.
Solution
First, find the instantaneous voltage in the coil with respect to time and angular velocity. Then, find the emf induced in the coil due to the change in current with respect to inductance and the rate of change of inductance. Then, apply Kirchhoff’s law and integrate the equations which conclude the result that voltage leads current by 2π, when A.C. voltage applied to pure inductance.
Complete step-by-step answer:
Instantaneous voltage )
Voltage,
V=2πsinωt
Where, ω is the angular velocity, t is the time.
e=LdtdI
Where, L is the inductance.
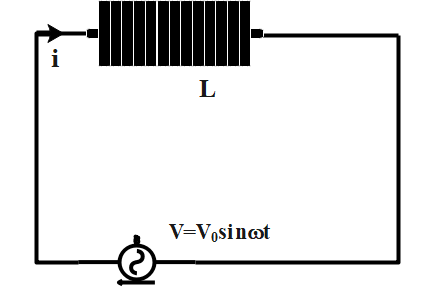
V = 2πsinωt----- (1)
Let this be equation (1)
Where,
ω = 2πf
Voltage across the coil varies with time and the varying current induces an emf in the coil
From the Kirchhoff’s law, we can write
V e = 0
Where, V is the voltage
e is the emf induced due to change in current
V = e----- (2)
Let this be equation (2)
Substitute the value of e as
e=LdtdIin equation (2)
We get,
V=LdtdI----- (3)
Let this be equation (3)
From the above equation, we obtain
dI= VLdt----- (4)
Let this be equation (4)
Substitute equation (1) in equation (4)
dI = LV0sinωtdt----- (5)
Let this be equation (5)
Integrating equation (5), we get
∫dI=LV0∫sinωtdt----- (6)
Let it be equation (6)
Where, I is the current
We get,
I=LVoω(−cosωt) -----(7)
Let it be equation (7)
Then substitute,
−cosωt=sin(wt−2π) in equation (7)
Let LωVo=I0 ----- (8)
Substitute equation (8) in equation (7)
We get,
I =Iosin(ωt−2π)----- (9)
Comparing equations (1) and (9),
We conclude that voltage leads current by 2π, when A.C. voltage applied to pure inductance
Hence, proved.
Note: There is also a case where current leads voltage in phase by 2π. This happens in certain cases where an ideal capacitor is used in an A.C. circuit .Therefore, current leads voltage in phase by 2π, in an A.C. circuit containing an ideal capacitor.
