Solveeit Logo
Login

Question

Question: Show that \(\vec a.(\vec b \times \vec c)\) is equal in magnitude to the volume of the parallelepipe...

Show that a⃗.(b⃗×c⃗)\vec a.(\vec b \times \vec c) is equal in magnitude to the volume of the parallelepiped formed on the three vectors a⃗\vec a,b⃗\vec b and c⃗\vec c

Explanation

Solution

The product of the area and altitude is known as the volume of the parallelepiped which is equal to the scalar triple product.Hence the vectors a⃗\vec a, b⃗\vec b and c⃗\vec c are parallelepiped. The vector product of the two vectors is known as the area of the parallelogram.

Complete step by step answer:
When the components are perpendicular to each other then it is called the rectangular components of the vector.

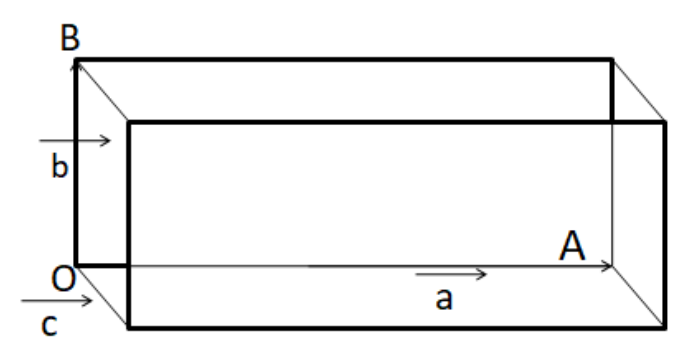
In the above diagram, the position vectors are,
OA=a⃗OA = \vec a
⇒OB=b⃗\Rightarrow OB = \vec b
⇒OC=c⃗\Rightarrow OC = \vec c
We know that the parallelepiped volume is equal to the product of the parallelogram area and its height.
Hence we can write the volume of the parallelepiped =a⃗.(b⃗×c⃗) = \vec a.(\vec b \times \vec c)……………….. (1)
Let us consider n⃗\vec n is the unit vector which is perpendicular to the b⃗\vec b and c⃗\vec c. The n⃗\vec n and c⃗\vec c have the unique direction. So we can write,
b⃗×c⃗=bcsin⁡θn^\vec b \times \vec c = bc\sin \theta \hat n
Here the angle, θ=90∘\theta = 90^\circ . Finally,
b⃗×c⃗=bcn^\vec b \times \vec c = bc\hat n …….(2)
Using the equation (1) the parallelepiped volume is =a⃗.(b⃗×c⃗) = \vec a.(\vec b \times \vec c)

Now we have to substitute the equation (2) into the equation (1) we get,
the parallelepiped volume is,
a⃗.(bcn^)=abccos⁡θn^\vec a.(bc\hat n) = abc\cos \theta \hat n
The n^\hat n is the unit vector so the angle becomes, θ=0∘\theta = 0^\circ . Hence the parallelepiped volume becomes, abcabc. And, the given parallelepiped volume is abcabc .From this explanation a⃗.(b⃗×c⃗)\vec a.(\vec b \times \vec c) is equal to the parallelepiped volume.

Note: The three vectors are parallelepiped which means the vectors are present in the same plane which is a coplanar vector. In some particulars, the length of the vectors may be zero. The scalar is a component that has the only component which is the magnitude and the vector has the two components to specify which is a magnitude and the direction.