Question

Show that the volume of the greatest cylinder which can be inscribed in a cone of height h and semi-vertical angle $\alpha \;{\text{is }}\dfrac{4}{{27}}\pi {h^3}{\tan ^2}\alpha$

Answer 1

Hint : First of all with the help of the given data, draw the diagram cylinder inscribed in the cone. Then use the formula for the volume of the cylinder, $V = \pi {r^2}h$ and use appropriate trigonometric relation to simplify the equation.

Complete step-by-step answer :
First of all draw the diagram with the help of the given conditions.
Cylinder is inscribed in the cone with the height “h”

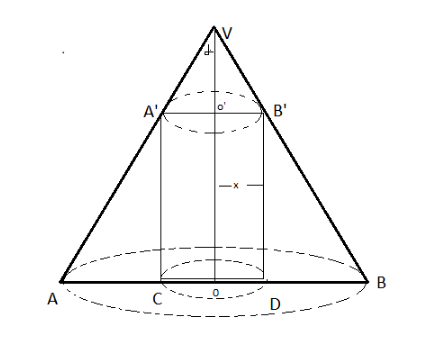
Let us assume that VAB be the given cone of height “h”, with the semi vertical angle $\alpha$ and let us also assume that “x” be the radius of the base of the cylinder A’B’CD which is inscribed in the cone.
Height of the cone $= h$
Height of the cylinder $= h - x\cot \alpha$
Now, volume of the cylinder is –
$V = \pi {r^2}h$
Place the values in the above equation –
$V = \pi {x^2}(h - x\cot \alpha )$ ..... (A)
Take the derivative of the volume with respect to “x”
$\Rightarrow \dfrac{{dV}}{{dx}} = 2\pi xh - 3\pi {x^2}\cot \alpha$ ..... (B)
Now, for the minimum of volume, above equation must satisfy $\dfrac{{dV}}{{dx}} = 0$
$\Rightarrow 0 = 2\pi xh - 3\pi {x^2}\cot \alpha$
Simplify and make “x” the subject –
$\Rightarrow 2\pi xh = 3\pi {x^2}\cot \alpha$
Common multiples from both the sides of the equation cancel each other –
$\Rightarrow 2h = 3x\cot \alpha$
$\Rightarrow x = \dfrac{{2h}}{{3\cot \alpha }}$
We know that cot is the inverse function of tangent.
$\Rightarrow x = \dfrac{{2h}}{3}\tan \alpha$ .... (C)
Take derivative of the equation (B) –
$\Rightarrow \dfrac{{{d^2}V}}{{d{x^2}}} = 2\pi h - 6\pi x\cot \alpha$
Substitute the values from equation (C) in the above equation –
$\Rightarrow \dfrac{{{d^2}V}}{{d{x^2}}} = \pi [2h - 4h]$
Simplify the above equation –
$\Rightarrow \dfrac{{{d^2}V}}{{d{x^2}}} = - 2\pi h < 0$
Hence, volume is maximum when $x = \dfrac{{2h}}{3}\tan \alpha$
Place the values in equation (A)
The maximum volume of cylinder is –
$V = \pi {\left( {\dfrac{{2h}}{3}\tan \alpha } \right)^2}\left( {h - \dfrac{{2h}}{3}} \right)$
Simplify the above equation –
$V = \pi {\left( {\dfrac{{2h}}{3}\tan \alpha } \right)^2}\left( {\dfrac{h}{3}} \right)$
Apply square inside the bracket –
$\Rightarrow V = \pi \left( {\dfrac{{4{h^2}}}{9}{{\tan }^2}\alpha } \right)\left( {\dfrac{h}{3}} \right)$
Find the product of both the brackets on right hand side of the equation –
$\Rightarrow V = \dfrac{4}{{27}}\pi {h^3}{\tan ^2}\alpha$
Hence, proved.

Note : Know the difference between the inscribed and circumscribed of the objects and apply accordingly. Inscribed figure is the shape drawn inside another shape whereas, the circumscribed is the shape drawn outside another shape.