Question

Show that the trajectory of a particle that is launched at an angle is parabolic?

Answer 1

First we have to draw a rough diagram of the path followed by the particle after projection showing all the required parameters. With the help of the known values in the x direction write the displacement along the x-axis where we will get the rime taken by the particle similarly write the displacement along the y-axis. Now on further solving we will get the equation which is equal to the general equation of parabola.

Complete step by step answer:
As per the given problem we have to prove that the trajectory of a particle is parabolic. Let a particle is projected with an initial speed of ${\text{u}}\,{\text{m}}{{\text{s}}^{{\text{ - 1}}}}$ which is inclined at an angle of ${\text{\theta }}$ with the horizontal line or we can say along x direction.

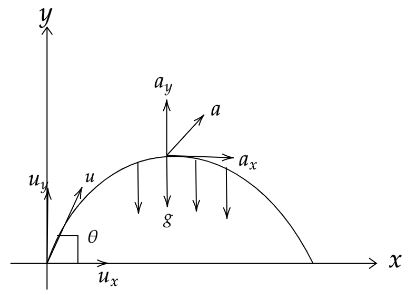
As the particle is projected at an angle then the speed and acceleration is splitted into two components.
The vertical component of $u$, ${u_y} = u\sin \theta$
The horizontal component of $u$, ${u_x} = u\cos \theta$
The acceleration on horizontal direction, ${a_x} = 0$
The acceleration along vertical direction, ${a_y} = - g$
Now using the displace formula of motion,
$s = ut + \dfrac{1}{2}a{t^2}$
Where, the displacement of the particle is $s$. Initial speed of the particle is $u$. Acceleration of the particle is $a$. Time taken by the particle is $t$.

Now putting the respective component in the above formula along x axis we will get,
$x = {u_x}t + \dfrac{1}{2}{a_x}{t^2}$
Now putting the respective values we will get,
$x = u\cos \theta t + \dfrac{1}{2}\left( 0 \right){t^2}$
$\Rightarrow x = u\cos \theta t$
Rearranging the above equation we will get,
$t = \dfrac{x}{{u\cos \theta }} \ldots \ldots \left( 1 \right)$
Now putting the respective component in the above displacement formula along y axis we will get,
$y = {u_y}t + \dfrac{1}{2}{a_y}{t^2}$
Now putting the respective values we will get,
$y = u\sin \theta t + \dfrac{1}{2}\left( { - g} \right){t^2}$

Now putting equation $\left( 1 \right)$ in the above equation we will get,
$y = u\sin \theta \left( {\dfrac{x}{{u\cos \theta }}} \right) + \dfrac{1}{2}\left( { - g} \right){\left( {\dfrac{x}{{u\cos \theta }}} \right)^2}$
Cancelling the common terms and on further calculation we will get,
$y = \tan \theta \cdot x - \dfrac{1}{2}g\dfrac{{{x^2}}}{{{u^2}{{\cos }^2}\theta }}$
Now comparing this equation with the standard equation of parabola we will get,
$y = a{x^2} + bx + c$
Where, a, b and c are constant.
On comparing we will get,
$a = - \dfrac{1}{2}g \times \dfrac{1}{{{u^2}{{\cos }^2}\theta }}$
$b = \tan \theta$
And $c = 0$

Hence proved that the trajectory of a particle projected at an angle is parabolic.

Note: The speed along the horizontal direction is constant that’s why the acceleration along the horizontal direction is zero and the vertical acceleration is opposite to the acceleration due to gravity that’s why it is taken as negative. Here the trajectory is the path followed by a particle when it is projected.