Question

Show that the time period ($T$) of a freely suspended magnetic dipole of magnetic moment ($M$) in a uniform magnetic field ($B$) given by, $T = 2\pi \sqrt {\dfrac{I}{{MB}}}$, where $I$ is the moment of inertia of the magnetic dipole.

Answer 1

A magnetic dipole in uniform magnetic field behaves similar to an electric dipole in uniform electric field. We can compare the calculations to an angular simple harmonic motion. A torque will be induced in the dipole due to the magnetic field applied on the dipole.

Formula used:
$\tau = \overrightarrow M \times \overrightarrow B$
${\omega ^2} = \dfrac{{MB}}{I}$

Complete step by step Solution:

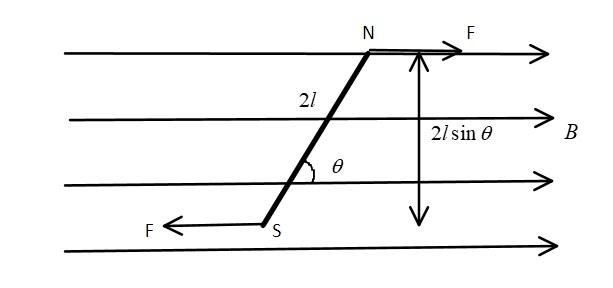
A magnetic dipole is an arrangement of two opposite magnetic poles, normally referred to as North and South, separated by a distance, $2l$. Both the poles are of equal magnitude and opposite in nature.
Whereas, when we look at magnetic dipole moment, it is defined as the product of magnitude of pole strength of any one of the poles with the distance of separation between the poles. Magnetic dipole moment is given by,
$M = m\left( {2l} \right)$, $m$ = $pole strength$
Here, in this case the dipole experiences a torque due to the applied magnetic field. We know that torque can be calculated by the product of force applied and perpendicular distance between the forces. Torque is given by the formula,
$\tau = 2lsin\theta \times \overrightarrow F$
Now, force of magnetic dipole is given by the product of magnitude of magnetic pole strength of any one pole and magnetic field applied. It is given by,
$\overrightarrow F = mB$
We can simply substitute this value of $\overrightarrow F$in the torque equation and we get,
$\tau = (m.B) \times 2lsin\theta$
As we can see here, $m(2l)$ is the magnetic dipole moment according to the definition, hence we can replace this term with magnetic dipole moment $M$ and the equation becomes,
$\tau = M.Bsin\theta$ , or $\tau = \overrightarrow M \times \overrightarrow B$ , which is the cross product form of the above equation.
Now, since the dipole experiences a torque, it also experiences angular acceleration when the value of $\theta$ keeps changing. This is due to the moment of inertia of magnetic dipole and hence it keeps oscillating. Considering these factors, the equation of torque was found to be,
$\tau = I\alpha$
Here, $I$ is the moment of inertia of the dipole and $\alpha$is the angular acceleration of the dipole. Now we can combine both the equations of torque and we get,
$MBsin\theta = I\alpha$
For small angle $\theta$, we get,
$MB\theta = I\alpha$, or
$\Rightarrow \alpha = \dfrac{{MB}}{I}\theta$
Now, $\theta$ will be the angular displacement of the dipole, since the dipole undergoes oscillations which are of angular simple harmonic motion. We can compare the equations of simple harmonic motion with $\alpha$. Comparing we see that,
$\alpha = {\omega ^2}\theta$, or
${\omega ^2} = \dfrac{{MB}}{I}$ , where $\omega$ is the angular frequency.
And in simple harmonic motion, the time period of the oscillations is given by the formula,
$T = \dfrac{2\pi}{\omega}$

Therefore, on substituting the value of $\omega$ we get the time period of the dipole as, $T = 2\pi \sqrt {\dfrac{I}{{MB}}}.$

Note: The magnetic dipole moment is analogous to electric dipole moment. Mostly, magnetic equations have similar analogy in electric equations. The magnetic field can also be written in terms of time period as $B = \dfrac{{4{\pi ^2}I}}{{M{T^2}}}.$