Question

Show that the solution set of the following linear inequations is empty set:
(i) $x-2y\ge 0$, $2x-y\le -2$, $x\ge 0$, $y\ge 0$.
(ii) $x-2y\le 3$, $3x+4y\ge 12$, $y\ge 1$, $x\ge 0$, $y\ge 0$.

Answer 1

We start solving the problem by substituting the point $\left( 0,0 \right)$ in the each given inequality in order to find whether the point is present inside its feasible region. We then plot all the inequalities on the graph showing all the feasible regions. We then check the intersection region of all the feasible regions to get our required solution set. We follow this process for both problems to get the result.

Complete step-by-step solution:
(i) According to the problem, we have inequalities $x-2y\ge 0$, $2x-y\le -2$, $x\ge 0$, $y\ge 0$ for which we need to show that the solution set is empty set.
Let us substitute the point $\left( 0,0 \right)$ in the inequality $x-2y\ge 0$.
$\Rightarrow 0-2\left( 0 \right)\ge 0$.
$\Rightarrow 0\ge 0$ (true). So, the point $\left( 0,0 \right)$ is in the solution set of $x-2y\ge 0$.
Let us substitute the point $\left( 0,0 \right)$ in the inequality $2x-y\le -2$.
$\Rightarrow 2\left( 0 \right)-0\le -2$.
$\Rightarrow 0\le -2$ (false). So, the point $\left( 0,0 \right)$ is in the solution set of $2x-y\le -2$.
Let us plot both inequalities in the graph.

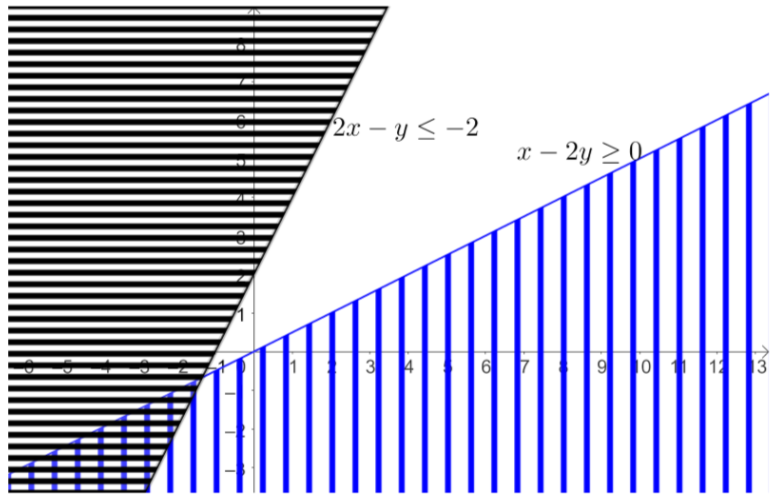
From the plot, we can see that both the inequalities do not have any intersection for $x\ge 0$, $y\ge 0$.
So, there is no feasible region to have a solution, which makes the solution set empty.
$\therefore$ We have proved that the solution set for $x-2y\ge 0$, $2x-y\le -2$, $x\ge 0$, $y\ge 0$ is empty set.

(ii) According to the problem, we have inequalities $x+2y\le 3$, $3x+4y\ge 12$, $y\ge 1$, $x\ge 0$, $y\ge 0$. for which we need to show that the solution set is empty set.
Let us substitute the point $\left( 0,0 \right)$ in the inequality $x+2y\le 3$.
$\Rightarrow 0+2\left( 0 \right)\le 3$.
$\Rightarrow 0\le 3$ (true). So, the point $\left( 0,0 \right)$ is in the solution set of $x+2y\le 3$.
Let us substitute the point $\left( 0,0 \right)$ in the inequality $3x+4y\ge 12$.
$\Rightarrow 3\left( 0 \right)+4\left( 0 \right)\ge 12$.
$\Rightarrow 0\ge 12$ (false). So, the point $\left( 0,0 \right)$ is in the solution set of $3x+4y\ge 12$.
Let us plot both inequalities in the graph.

From the plot, we can see that both the inequalities do not have any intersection for $x\ge 0$, $y\ge 0$.
So, there is no feasible region to have a solution, which makes the solution set empty.
$\therefore$ We have proved that the solution set for $x+2y\le 3$, $3x+4y\ge 12$, $y\ge 1$, $x\ge 0$, $y\ge 0$ is empty set.

Note: We should not forget to plot the inequality $y\ge 1$ while solving problem (ii). We should know that the x and y co-ordinate of every point in the feasible region (common intersection of all regions) should be positive. We should make mistake while noting the equation of inequality. If we get any feasible region, then we find the value of the objective function (if given) at the corner points of the feasible region.