Question

Show that the semi-vertical angle of the cone of the maximum volume and given slant height is ${{\cos }^{-1}}\dfrac{1}{\sqrt{3}}$.

Answer 1

We will use the formula for the volume of the cone, which is given by $V=\dfrac{1}{3}\pi {{r}^{2}}h$. We have a given slant height. So we will use the trigonometric relations to rewrite the radius and height in the formula of the volume in terms of slant height and the semi-vertical angle of the cone. We will find the maximum volume of the cone by differentiating it and equating it to zero. Using this information, we will be able to calculate the semi-vertical angle of this cone.

Complete step-by-step solution
The volume of the cone is given by $V=\dfrac{1}{3}\pi {{r}^{2}}h$ where $h$ is the height of the cone and $r$ is the radius of the base. Now, let us look at a diagram of the cone.

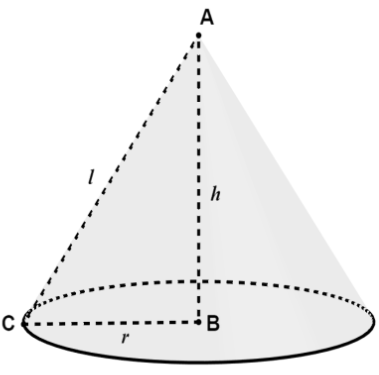
We have a triangle formed by the radius, height, and slant height of the cone. The radius and height are perpendicular to each other. In the right-angled triangle $\Delta ABC$, let the semi-vertical angle $\angle BAC$ be denoted by $\theta$. In $\Delta ABC$, using the trigonometric relations, we can write
$\sin \theta =\dfrac{r}{l}$ and $\cos \theta =\dfrac{h}{l}$. Therefore, we have $r=l\sin \theta$ and $h=l\cos \theta$. Substituting these values of radius and height in the formula for the volume of the cone, we get
$\begin{aligned} & V=\dfrac{1}{3}\pi {{\left( l\sin \theta \right)}^{2}}\left( l\cos \theta \right) \\\ & =\dfrac{1}{3}\pi {{l}^{3}}{{\sin }^{2}}\theta \cos \theta \end{aligned}$
Now, we want to maximize the volume of the cone. The volume is maximum when $\dfrac{dV}{d\theta }=0$. Differentiating the volume of the cone with respect to the semi-vertical angle, we get the following expression,
$\begin{aligned} & \dfrac{dV}{d\theta }=\dfrac{d}{d\theta }\left( \dfrac{1}{3}\pi {{l}^{3}}{{\sin }^{2}}\theta \cos \theta \right) \\\ & =\dfrac{1}{3}\pi {{l}^{3}}\dfrac{d}{d\theta }\left( {{\sin }^{2}}\theta \cos \theta \right) \end{aligned}$
We know that $\dfrac{d}{dx}\left( f\left( x \right)\cdot g\left( x \right) \right)=f\left( x \right)\dfrac{d}{dx}\left( g\left( x \right) \right)+g\left( x \right)\dfrac{d}{dx}\left( f\left( x \right) \right)$. Applying this rule to the above expression, we get
$\begin{aligned} & \dfrac{dV}{d\theta }=\dfrac{1}{3}\pi {{l}^{3}}\dfrac{d}{d\theta }\left( {{\sin }^{2}}\theta \cos \theta \right) \\\ & =\dfrac{1}{3}\pi {{l}^{3}}\left[ {{\sin }^{2}}\theta \dfrac{d}{d\theta }\left( \cos \theta \right)+\cos \theta \dfrac{d}{d\theta }\left( {{\sin }^{2}}\theta \right) \right] \end{aligned}$
We know that $\dfrac{d}{d\theta }\left( \cos \theta \right)=-\sin \theta$ and $\dfrac{d}{d\theta }\left( {{\sin }^{2}}\theta \right)=2\sin \theta \cos \theta$. Substituting these values in the above equation, we get
$\begin{aligned} & \dfrac{dV}{d\theta }=\dfrac{1}{3}\pi {{l}^{3}}\left[ {{\sin }^{2}}\theta \left( -\sin \theta \right)+\cos \theta \left( 2\sin \theta \cos \theta \right) \right] \\\ & =\dfrac{1}{3}\pi {{l}^{3}}\left[ -{{\sin }^{3}}\theta +2\sin \theta {{\cos }^{2}}\theta \right] \\\ & =\dfrac{1}{3}\pi {{l}^{3}}\sin \theta \left[ -{{\sin }^{2}}\theta +2{{\cos }^{2}}\theta \right] \end{aligned}$
We also know that ${{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1$. So, we will substitute $-{{\sin }^{2}}\theta ={{\cos }^{2}}\theta -1$ in the above equation, we get
$\begin{aligned} & \dfrac{dV}{d\theta }=\dfrac{1}{3}\pi {{l}^{3}}\sin \theta \left[ {{\cos }^{2}}\theta -1+2{{\cos }^{2}}\theta \right] \\\ & =\dfrac{1}{3}\pi {{l}^{3}}\sin \theta \left[ 3{{\cos }^{2}}\theta -1 \right] \end{aligned}$
Now, we will equate the above equation to zero.
$\dfrac{1}{3}\pi {{l}^{3}}\sin \theta \left[ 3{{\cos }^{2}}\theta -1 \right]=0$
So, this implies that either $\sin \theta =0$ or $3{{\cos }^{2}}\theta -1=0$.
We know that if $\sin \theta =0$, then $\theta =0{}^\circ$. We will have to discard this possibility because the semi-vertical angle of a cone cannot be $\theta =0{}^\circ$. So, the only possibility is $3{{\cos }^{2}}\theta -1=0$.
This implies that ${{\cos }^{2}}\theta =\dfrac{1}{3}$. So, we have $\cos \theta =\dfrac{1}{\sqrt{3}}$. Therefore, we have the semi-vertical angle as $\theta ={{\cos }^{-1}}\dfrac{1}{\sqrt{3}}$. Hence, proved.

Note: It is important to understand that we get the critical points of a function $f\left( x \right)$ by equating the derivative to zero, $\dfrac{d}{dx}f\left( x \right)=0$. The critical point tells us that the function can have either a maximum value or a minimum value at that point. To check whether the critical point is a maximum or a minimum, we compute the second derivative of that function. If the second derivative is positive, then the critical point is a local minimum and if it is negative, then the critical point is a local maximum. This is called the second derivative test.