Question

Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is ${{\tan }^{-1}}\sqrt{2}$.

Answer 1

To solve this problem we should have basic knowledge about trigonometry and geometry. To solve this first of all we will assume the height, slant height and radius of the cone as h, l and r respectively. Then we will express h and r in terms of l using angle $\theta$ i.e. semi-vertical angle of the cone then we will find the volume of the cone using formula $V=\dfrac{1}{3}\pi {{r}^{2}}h$, and then we will take derivative of volume w.r.t angle $\theta$ and then observe where derivative changes sign to find the maxima.

Complete step by step answer:
We have to prove that the semi-vertical angle of the cone of the maximum volume and of given slant height is ${{\tan }^{-1}}\sqrt{2}$.
So first of all for better understanding we will draw the diagram as follows,

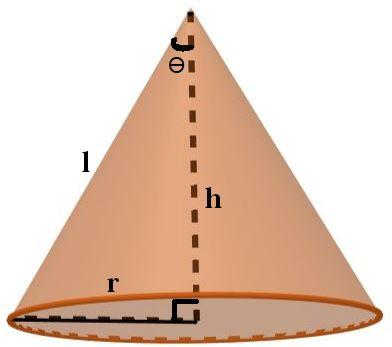
We have assumed height, slant height and radius as h, l and r respectively.
We know that in the figure,
$\begin{aligned} & \sin \theta =\dfrac{r}{l} \\\ & \Rightarrow r=l\sin \theta \,\,.....\left( 1 \right) \\\ \end{aligned}$
And,
$\begin{aligned} & \cos \theta =\dfrac{h}{l} \\\ & \Rightarrow h=l\cos \theta \,\,.....\left( 2 \right) \\\ \end{aligned}$
And we know that volume of a cone is given as,
$V=\dfrac{1}{3}\pi {{r}^{2}}h$
Using equation 1 and 2 we get,
\Rightarrow $$$V=\dfrac{1}{3}\pi {{\left( l\sin \theta \right)}^{2}}\left( l\cos \theta \right)$ $\Rightarrow $ $V=\dfrac{1}{3}\pi {{l}^{3}}{{\sin }^{2}}\theta \cos \theta $ Now to find the maxima we will have to differentiate the above expression as, $\dfrac{dv}{d\theta }=\dfrac{1}{3}\pi {{l}^{3}}\left( 2\sin \theta \cos \theta .\cos \theta +{{\sin }^{2}}\theta \left( -\sin \theta \right) \right)$ $\Rightarrow $ $\dfrac{dv}{d\theta }=\dfrac{1}{3}\pi {{l}^{3}}\left( 2\sin \theta {{\cos }^{2}}\theta -{{\sin }^{3}}\theta \right)$ Taking \sin \theta as common, we get $\Rightarrow $ $\dfrac{dv}{d\theta }=\dfrac{1}{3}\pi {{l}^{3}}\sin \theta \left( 2{{\cos }^{2}}\theta -{{\sin }^{2}}\theta \right)$ We know that $\left( {{a}^{2}}-{{b}^{2}} \right)=\left( a+b \right)\left( a-b \right)$, hence we get $\Rightarrow $ $\dfrac{dv}{d\theta }=\dfrac{1}{3}\pi {{l}^{3}}\sin \theta \left( \sqrt{2}\cos \theta -\sin \theta \right)\left( \sqrt{2}\cos \theta +\sin \theta \right)$ Dividing and multiplying by $\cos \theta $, we get $\Rightarrow $ $\dfrac{dv}{d\theta }=\dfrac{1}{3}\pi {{l}^{3}}\sin \theta .{{\cos }^{2}}\theta \dfrac{\left( \sqrt{2}\cos \theta -\sin \theta \right)}{\cos \theta }\dfrac{\left( \sqrt{2}\cos \theta +\sin \theta \right)}{\cos \theta }$ $\Rightarrow $$$\dfrac{dv}{d\theta }=\dfrac{1}{3}\pi {{l}^{3}}\sin \theta .{{\cos }^{2}}\theta \left( \sqrt{2}-\tan \theta \right)\left( \sqrt{2}+\tan \theta \right)
Now at maxima $\dfrac{dv}{d\theta }=0$, we get
\Rightarrow $$$\dfrac{1}{3}\pi {{l}^{3}}\sin \theta .{{\cos }^{2}}\theta \left( \sqrt{2}-\tan \theta \right)\left( \sqrt{2}+\tan \theta \right)=0$$ We know that {{0}^{\circ }}<\theta <{{90}^{\circ }}$, so in the above equation,$\begin{aligned}
& \sin \theta =+ve \\
& \cos \theta =+ve \\
& \sqrt{2}+\tan \theta =+ve \\
\end{aligned}$As all$\sin \theta ,cos\theta ,and,tan\theta $are positive in the interval. But for the term$\left( \sqrt{2}-\tan \theta \right)$, we have

& \Rightarrow \dfrac{dv}{d\theta }=+ve\,\,\,\left( for\,\tan \theta <\sqrt{2} \right) \\\ & \Rightarrow \dfrac{dv}{d\theta }=-ve\,\,\,\left( for\,\tan \theta >\sqrt{2} \right) \\\ \end{aligned}$$ Hence $$\dfrac{dv}{d\theta }$$ changes sign from positive to negative hence this is maxima, so we get $$\begin{aligned} & \tan \theta =\sqrt{2} \\\ & \Rightarrow \theta ={{\tan }^{-1}}\sqrt{2} \\\ \end{aligned}$$ Hence proved. **Note:** To solve these kinds of questions you need to have basic knowledge about trigonometry, geometry and also you should know how to find the maxima, minima using the first derivative test. If you don’t know then kindly go through these topics and try again to solve this problem. As this problem involves a lot of calculation so you need to be careful about this while solving.