Question

Show that the points $\left( {12,8} \right)$ , $\left( { - 2,6} \right)$ and $\left( {6,0} \right)$ are the vertices of right angled triangle and also show that the midpoint of the hypotenuse is equidistant from the angular points.

Answer 1

Hint : Here we are given with three points and their coordinates also. To show that they are the vertices of a right angled triangle we have to prove that the distances between the points that form the sides of the triangle are in a Pythagorean triplet. If they form a triplet then that triangle is definitely a right angled triangle.
And to prove that the angular points of hypotenuse are equidistant from the midpoint of hypotenuse we will use the midpoint formula to find the value of midpoint and then distance formula to find the distance.
Formula used:
Distance between two points with coordinates $\left( {{x_1},{y_1}} \right)\& \left( {{x_2},{y_2}} \right)$ is given by
$d = \sqrt {{{\left( {{x_2} - {x_1}} \right)}^2} + {{\left( {{y_2} - {y_1}} \right)}^2}}$

Complete step by step solution:
We are given three points. Let $A\left( {12,8} \right),B\left( { - 2,6} \right)\& C\left( {6,0} \right)$ be the vertices.

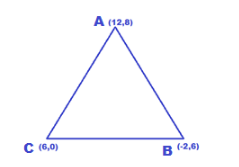
Now let’s find the distances $AB,BC\& CA$ using distance formula.
$d\left( {AB} \right) = \sqrt {{{\left( { - 2 - 12} \right)}^2} + {{\left( {6 - 8} \right)}^2}}$
On solving the brackets we get,
$d\left( {AB} \right) = \sqrt {{{\left( { - 14} \right)}^2} + {{\left( { - 2} \right)}^2}}$
Taking the squares we get,
$d\left( {AB} \right) = \sqrt {196 + 4}$
On adding
$d\left( {AB} \right) = \sqrt {200}$
The root can be simplified as,
$d\left( {AB} \right) = \sqrt {100 \times 2} = 10\sqrt 2$
This is the distance between points A and B.
Now let’s find the remaining distances.
$d\left( {BC} \right) = \sqrt {{{\left( {6 - \left( { - 2} \right)} \right)}^2} + {{\left( {0 - 6} \right)}^2}}$
On solving the brackets we get,
$d\left( {BC} \right) = \sqrt {{{\left( 8 \right)}^2} + {{\left( { - 6} \right)}^2}}$
Taking the squares,
$d\left( {BC} \right) = \sqrt {64 + 36}$
On adding the terms,
$d\left( {BC} \right) = \sqrt {100}$
Taking the root,
$d\left( {BC} \right) = 10$
And now the last distance,
$d\left( {CA} \right) = \sqrt {{{\left( {6 - 12} \right)}^2} + {{\left( {0 - 8} \right)}^2}}$
On solving the brackets we get,
$d\left( {CA} \right) = \sqrt {{{\left( { - 6} \right)}^2} + {{\left( { - 8} \right)}^2}}$
Taking the squares,
$d\left( {CA} \right) = \sqrt {36 + 64}$
On adding the terms,
$d\left( {CA} \right) = \sqrt {100}$
Taking the root,
$d\left( {CA} \right) = 10$

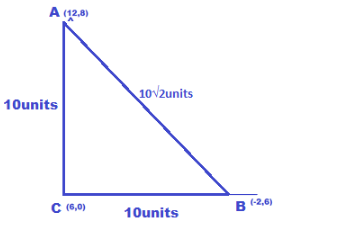
Now if we check for the triplet we get,
$d\left( {AB} \right) = \sqrt {d{{\left( {BC} \right)}^2} + d{{\left( {CA} \right)}^2}}$
That is putting the values of distances,
$10\sqrt 2 = \sqrt {{{10}^2} + {{10}^2}}$
$10\sqrt 2 = \sqrt {100 + 100}$
On adding we get,
$10\sqrt 2 = \sqrt {200}$
$10\sqrt 2 = 10\sqrt 2$
Thus the vertices are in a Pythagorean triplet. So they are definitely the vertices of a right angled triangle.

PART 2 OF SOLUTION:
Now in order to check for the midpoint of hypotenuse to be equidistant from the angular points we will use the midpoint formula. First we will find the midpoint of the hypotenuse and then we will use distance formula.
Coordinates of the angular points are $A\left( {12,8} \right),B\left( { - 2,6} \right)$ . Using midpoint formula we get,
$\left( {x,y} \right) = \left( {\dfrac{{{x_1} + {x_2}}}{2},\dfrac{{{y_1} + {y_2}}}{2}} \right)$
Where x and y are the coordinates of the midpoint of the hypotenuse.
Putting the values of the coordinates we get,
$\left( {x,y} \right) = \left( {\dfrac{{12 + \left( { - 2} \right)}}{2},\dfrac{{8 + 6}}{2}} \right)$
On performing the mathematical operations
$\left( {x,y} \right) = \left( {\dfrac{{10}}{2},\dfrac{{14}}{2}} \right)$
On dividing by 2 we get,
$\left( {x,y} \right) = \left( {5,7} \right)$
These are the coordinates of the midpoint of hypotenuse.

The situation is depicted above. Now we will use the distance formula to find the distance of angular points from the midpoints.

Distance from A to midpoint is,	Distance from B to midpoint is,
$A \to mid-point = \sqrt {{{\left( {7 - 8} \right)}^2} + {{\left( {5 - 12} \right)}^2}}$ On taking the subtraction, $A \to mid-point = \sqrt {1 + {{\left( { - 7} \right)}^2}}$ Taking the square, $A \to mid-point = \sqrt {1 + 49}$ On adding we get, $A \to mid-point = \sqrt {50}$	$B \to mid-point = \sqrt {{{\left( {7 - 6} \right)}^2} + {{\left( {5 - \left( { - 2} \right)} \right)}^2}}$ On taking the subtraction we get, $B \to mid-point = \sqrt {1 + {{\left( 7 \right)}^2}}$ Taking the square, $B \to mid-point = \sqrt {1 + 49}$ On adding we get, $B \to mid-point = \sqrt {50}$

Thus the distances of the angular points are the same from the midpoint.

Note : Note that for the points to be vertices of a right angled triangle the only way is to show that the points are in a Pythagorean triplet. Here we are not given with any of the angular details so that we cannot lead with the way. Also note that angular points are nothing but the same points of the side of which equidistant is getting found and not the other side.
Also note that if all the sides are the same then that triangle is not a right angle triangle ; it will be an equilateral triangle.