Question

Show that the points (1, 2), (2, 1) and (-2, 5) are collinear.

Answer 1

Hint: To solve this problem, a distance formula between two points will be used. The distance formula between two points $\left( {{x_1},\;{y_1}} \right)\;and\;\left( {{x_2},\;{y_2}} \right)$ is-
$\mathrm d=\sqrt{\left({\mathrm x}_2-{\mathrm x}_1\right)^2+\left({\mathrm y}_2-{\mathrm y}_1\right)^2}$

Let the points be A(1, 2), B(2, 1) and C(-2, 5).

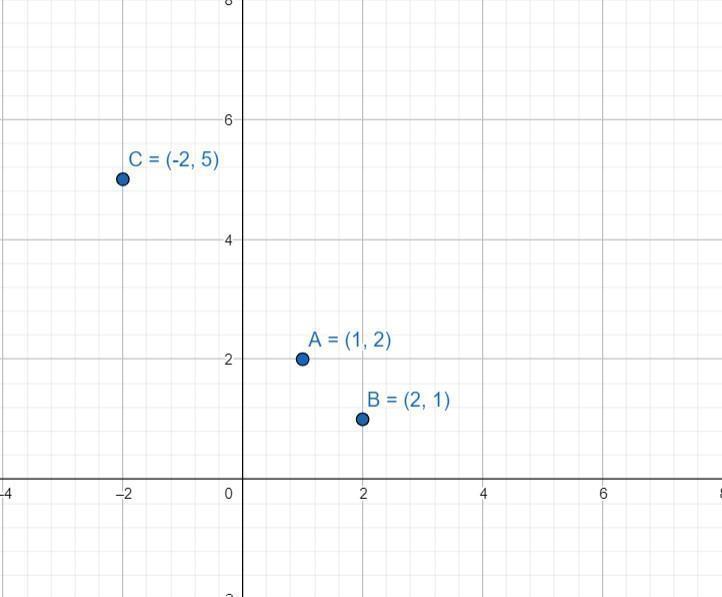
For these points to be collinear, it is sufficient to prove that BA + AC = BC. By applying distance formula in these three points-
$\begin{aligned} &BA; = \sqrt {{{\left( {2 - 1} \right)}^2} + {{\left( {1 - 2} \right)}^2}} \\\ &= \sqrt {{1^2} + {{\left( { - 1} \right)}^2}} = \sqrt 2 \\\ ∾ = \sqrt {{{\left( {1 - \left( { - 2} \right)} \right)}^2} + {{\left( {2 - 5} \right)}^2}} \\\ &= \sqrt {{3^2} + {{\left( { - 3} \right)}^2}} = \sqrt {18} = 3\sqrt 2 \\\ &BC; = \sqrt {{{\left( {2 - \left( { - 2} \right)} \right)}^2} + {{\left( {1 - 5} \right)}^2}} \\\ &= \sqrt {{4^2} + {{\left( { - 4} \right)}^2}} = \sqrt {32} = 4\sqrt 2 \\\ &BA; \+ AC = \sqrt 2 + 3\sqrt 2 = 4\sqrt 2 = BC \\\ \end{aligned}$
Hence, the three points A, B, C are collinear. Hence, proved.

Note: The points can also be proved collinear using the triangle formula. We can prove the area of the triangle formed by these three points to be zero, which means they are collinear. The area of triangle formed by three points $\left( {{{\text{x}}_1},\;{{\text{y}}_1}} \right),\left( {{{\text{x}}_2},\;{{\text{y}}_2}} \right)\;and\;\left( {{{\text{x}}_3},\;{{\text{y}}_3}} \right)$ is-
${{\text{x}}_1}\left( {{{\text{y}}_2} - {{\text{y}}_3}} \right) + {{\text{x}}_2}\left( {{{\text{y}}_3} - {{\text{y}}_1}} \right) + {{\text{x}}_3}\left( {{{\text{y}}_1} - {{\text{y}}_2}} \right)$
Applying this formula-
=1(1 - 5) + 2(5 - 2) - 2(2 - 1)
= -4 + 6 - 2
= 0
Hence, proved.