Question

Show that the path of a moving point, such that its distance from two lines $3x - 2y = 5$ and $3x + 2y = 5$ are equal is a straight line.

Answer 1

In the above question, we are given two straight lines $3x - 2y = 5$ and $3x + 2y = 5$ . We have to find the equation of a straight line that is equidistant from both the above-given lines. We can use the following formula to find the distance of a point on the new straight line from the given two lines.

The distance from a point $(h,k)\;$ to a straight line $ax + by + c = 0$ is given by the formula :
$\Rightarrow d = \dfrac{{\left| {ah + bk + c} \right|}}{{\sqrt {{a^2} + {b^{^2}}} }}$

Complete step-by-step solution:
Given two straight lines are $3x - 2y = 5$ and $3x + 2y = 5$
We can also write is as,
$\Rightarrow 3x - 2y - 5 = 0$ and $\Rightarrow 3x + 2y - 5 = 0$
Let the point $(h,k)\;$ be any point which is equidistant from both the lines $3x - 2y - 5 = 0$ and $3x + 2y - 5 = 0$ .
Now using the formula of distance between a point and a straight line, that is
$\Rightarrow d = \dfrac{{\left| {ah + bk + c} \right|}}{{\sqrt {{a^2} + {b^{^2}}} }}$
Hence, the distance of point $(h,k)\;$ from the straight line $3x - 2y - 5 = 0$ is given by
$\Rightarrow {d_1} = \dfrac{{\left| {3h - 2k - 5} \right|}}{{\sqrt {{3^2} + {{\left( { - 2} \right)}^{^2}}} }}$
Or,
$\Rightarrow {d_1} = \dfrac{{\left| {3h - 2k - 5} \right|}}{{\sqrt {9 + 4} }}$
So,
$\Rightarrow {d_1} = \dfrac{{\left| {3h - 2k - 5} \right|}}{{\sqrt {13} }}$
Similarly, the distance of point $(h,k)\;$ from the straight line $3x + 2y - 5 = 0$ is given by,
$\Rightarrow {d_2} = \dfrac{{\left| {3h + 2k - 5} \right|}}{{\sqrt {{3^2} + {2^{^2}}} }}$
Or,
$\Rightarrow {d_2} = \dfrac{{\left| {3h + 2k - 5} \right|}}{{\sqrt {9 + 4} }}$
So,
$\Rightarrow {d_2} = \dfrac{{\left| {3h + 2k - 5} \right|}}{{\sqrt {13} }}$
Now since, $(h,k)\;$ is equidistant from both the lines $3x - 2y - 5 = 0$ and $3x + 2y - 5 = 0$ ,
Therefore we can write,
$\Rightarrow {d_1} = {d_2}$
That gives,
$\Rightarrow \dfrac{{\left| {3h - 2k - 5} \right|}}{{\sqrt {13} }} = \dfrac{{\left| {3h + 2k - 5} \right|}}{{\sqrt {13} }}$
Cancelling the common denominators, we get
$\Rightarrow \left| {3h - 2k - 5} \right| = \left| {3h + 2k - 5} \right|$
Removing the modulus sign, we can write
$\Rightarrow 3h - 2k - 5 = \pm \left( {3h + 2k - 5} \right)$
Case 1: If $3h - 2k - 5 = 3h + 2k - 5$
Then, we get
$\Rightarrow 3h - 2k - 5 = 3h + 2k - 5$
Removing the common terms, that gives
$\Rightarrow - 2k = 2k$
Or,
$\Rightarrow - k = k$
Therefore,
$\Rightarrow k = 0$
Taking locus of $k = 0$ we can write the equation of the straight line as
$\Rightarrow y = 0$
Case 2: If $3h - 2k - 5 = - \left( {3h + 2k - 5} \right)$
Then we get,
$\Rightarrow 3h - 2k - 5 = - \left( {3h + 2k - 5} \right)$
Or,
$\Rightarrow 3h - 2k - 5 = - 3h - 2k + 5$
Removing the common term, we can write
$\Rightarrow 3h - 5 = - 3h + 5$
That gives,
$\Rightarrow 6h = 10$
Or,
$\Rightarrow h = \dfrac{{10}}{6}$
Hence,
$\Rightarrow h = \dfrac{5}{3}$
Taking locus of $h = \dfrac{5}{3}$ we can write the equation of the straight line as,
$\Rightarrow x = \dfrac{5}{3}$
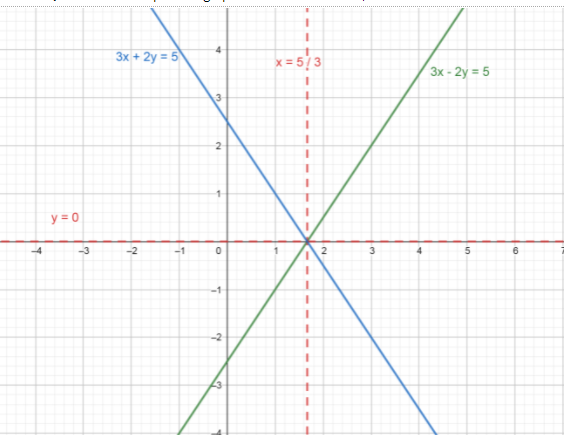
Hence, the two required straight lines, which are equidistant from the straight lines $3x - 2y = 5$ and $3x + 2y = 5$ are $y = 0$ and $x = \dfrac{5}{3}$ .

Therefore, the path of a moving point, such that its distance from two lines $3x - 2y = 5$ and $3x + 2y = 5$ are equal is a straight line.

Note: We can also plot the graph of the above lines as,