Question

Show that the motion of a simple pendulum is simple harmonic. Calculate the change in the length of a simple pendulum of length $l\,metres$ , when its period of oscillation changes from $2\,to\,1.5s$.

Answer 1

We start by writing down the given information. we then find the value of the weight of the bob and resolve it into its respective components. We then apply the second law of motion and find the relation between the acceleration of the bob and acceleration due to gravity. We then apply this acquired relation to the formula of the time period. We then find the change in length for both the time values and divide them.

Formulas used:
$T = 2\pi \sqrt {\dfrac{l}{g}}$
$\Rightarrow \theta = \dfrac{\text{arc}}{\text{radius}} = \dfrac{x}{l}$
$\Rightarrow W = mg$

Complete step by step answer:
Let the length of the thread suspending the bob be of $l\,metres$

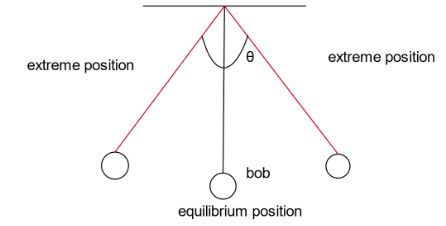
Let the bob be moving from one extreme to another. The restoring force acting on it makes it move from one extreme point to the next. Let the weight of the bob be given as $W = mg$.Now let us divide it into its components, $mg\sin \theta$ and $mg\cos \theta$.

The sine component will be responsible for the vertical movement and the cosine component will balance the tension in the string.Let us remember Newton’s second law.According to this law,
$mg\sin \theta = ma$
This gives us an expression for the acceleration of the bob, $g\sin \theta = a$. The value of the sine of any small angle will be the angle itself, hence we arrive at $g\theta = a$.

Now we find an expression for $\theta$ .
We know that $\theta = \dfrac{{arc}}{{radius}} = \dfrac{x}{l}$
Now the value of acceleration is,
$a = \dfrac{{g\left( x \right)}}{l}$
Since the value of acceleration due to gravity and the value of the length will remain a constant,
$a \propto x$
Since acceleration is proportional to displacement and acceleration is directed towards a fixed point the motion of the pendulum is "simple harmonic".

When the period of oscillation changes from $2\,to\,1.5s$: We know that the formula to find the period of a pendulum is given by,
$T = 2\pi \sqrt {\dfrac{l}{g}}$
When the period is $2s$ , $2 = 2\pi \sqrt {\dfrac{l}{g}}$
When the period is $1.5s$ , $1.5 = 2\pi \sqrt {\dfrac{l}{g}}$
We divide both of these to find the change in length of the pendulum
$\dfrac{2}{{1.5}} = \dfrac{1}{{\sqrt l }}$
$\dfrac{4}{3} = \dfrac{1}{{\sqrt l }}$
Squaring both sides, $l = \dfrac{9}{{16}} = 0.5625$
We have the changed length as $0.5625$.

Therefore, the change in the length of a simple pendulum of length $l\,metres$ , when its period of oscillation changes from $2\,to\,1.5s$ will be $1 - 0.5625$ which is $0.4375$.

Note: Simple harmonic motion is periodic to and fro motion or vibration of a particle.The value of $l\,metres$ is taken as one because then the value of the change in length can be found out without a problem. The squaring of the length of the pendulum must be done.