Question

Show that the maximum height and range of a projectile are $\dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$ and $\dfrac{{{u^2}\sin 2\theta }}{g}$ respectively?

Answer 1

Use the first and second kinematic equations. First determine the time required for the projectile to reach the maximum height using the first kinematic equation and then derive the equation for maximum height projectile using the second kinematic equation. Determine the time period of the projectile and then use a second j=kinematic equation to determine the horizontal range of the projectile.

Formulae used:
The kinematic equation relating final velocity $v$, initial velocity $u$, acceleration $a$ and time $t$ is
$v = u + at$ …… (1)
The kinematic equation relating displacement $s$, initial velocity $u$, acceleration $a$ and time $t$ is
$s = ut + \dfrac{1}{2}a{t^2}$ …… (2)

Complete step by step solution:
Let us assume that an object of mass $m$ is projected with velocity of projection $v$ and angle of projection $\theta$. Let $H$ be the maximum height attained by the projectile and $R$ be the range of the projectile.
The diagram of the projectile motion of the object is as follows:

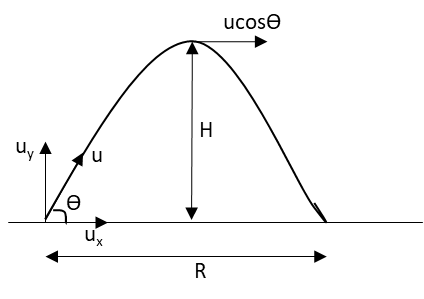
The initial horizontal and vertical component of the projectile are
${u_x} = u\cos \theta$
${u_y} = u\cos \theta$
The horizontal component of velocity of the projectile remains the same throughout the motion of the projectile.
${v_x} = u\cos \theta$
The vertical velocity of the projectile is zero at maximum height and the vertical acceleration of the projectile is $- g$.
Rewrite equation (1) for the final vertical velocity ${v_{ym}}$ of the projectile at maximum height.
${v_{ym}} = {u_y} + {a_y}t$
Substitute 0 for ${v_{ym}}$, $u\sin \theta$ for ${u_y}$ and $- g$ for ${a_y}$ in the above equation.
$0 = u\sin \theta - gt$
$\Rightarrow t = \dfrac{{u\sin \theta }}{g}$
This is the time required for the projectile to reach the maximum height.
Rewrite equation (2) for the maximum height of the projectile.
$H = {u_y}t + \dfrac{1}{2}{a_y}{t^2}$
Substitute $u\sin \theta$ for ${u_y}$, $- g$ for ${a_y}$ and $\dfrac{{u\sin \theta }}{g}$ for $t$ in the above equation.
$H = u\sin \theta \left( {\dfrac{{u\sin \theta }}{g}} \right) - \dfrac{1}{2}g{\left( {\dfrac{{u\sin \theta }}{g}} \right)^2}$
$\Rightarrow H = \dfrac{{{u^2}{{\sin }^2}\theta }}{g} - \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$
$\Rightarrow H = \dfrac{{{u^2}{{\sin }^2}\theta }}{{2g}}$
This is the required expression for the maximum height of the projectile.

The time period $T$ of the projectile is twice the time required for the projectile to reach the maximum height.
$T = \dfrac{{2u\sin \theta }}{g}$
Rewrite equation (1) for the displacement of the projectile equal to the range of projectile.
$R = {u_x}T + \dfrac{1}{2}{a_x}{T^2}$
The horizontal acceleration of the projectile is zero.
Substitute $u\cos \theta$ for ${u_x}$, $\dfrac{{2u\sin \theta }}{g}$ for $T$ and $0\,{\text{m/}}{{\text{s}}^2}$ for ${a_x}$ in the above equation.
$R = \left( {u\cos \theta } \right)\left( {\dfrac{{2u\sin \theta }}{g}} \right) + \dfrac{1}{2}\left( {0\,{\text{m/}}{{\text{s}}^2}} \right){\left( {\dfrac{{2u\sin \theta }}{g}} \right)^2}$
$\Rightarrow R = \dfrac{{2{u^2}\sin \theta \cos \theta }}{g} + 0$
$\Rightarrow R = \dfrac{{{u^2}\sin 2\theta }}{g}$
This is the required expression for the horizontal range of the projectile.

So, the correct answer is “Option D”.

Note:
The students should not forget to take the horizontal component of acceleration of the projectile as zero and the vertical component of the acceleration of projectile as the negative of acceleration due to gravity. Also, the students should not forget to use the vertical velocity of the projectile at maximum height as zero.