Question

Show that the magnetic field at the center of the circular coil in the figure is zero.

Answer 1

Hint : A magnetic field is a vector field that describes the magnetic influence on moving electric charges, electric currents, and magnetic materials. Oersted found that a magnetic field is established around a current carrying conductor.

Complete Step By Step Answer:
Biot-Savart’s law is used to determine the magnetic field at any point due to a current carrying conductor. This law is for infinitesimally small conductors yet it can be used for long conductors.
According to Biot-Savart’s Law, magnetic field at point $P$ due to the current element $i\overrightarrow {dl}$ is given by the expression,
$d\overrightarrow B = \dfrac{{{\mu _O}}}{{4\pi }}\dfrac{{idl\sin \theta }}{{{r^2}}}\hat n$
$\Rightarrow \vec B = \dfrac{{{\mu _O}i}}{{4\pi }}\int {\dfrac{{dl\sin \theta }}{{{r^2}}}} \hat n$
Where, $\vec B =$Magnetic field at point $P$
${\mu _O}$=Absolute permeability of vacuum$= 4\pi \times {10^{ - 7}}Wb{A^{ - 1}}{m^{ - 1}}$
$i =$Electric current in the conductor,
$dl =$Length of the conductor causing magnetic field,
$\theta =$The angle which that length makes at point $P$,
$r =$Distance of the conductor from point $P$, and
$\hat n =$The unit vector showing the direction of the magnetic field.
The direction of magnetic field is determined with the help of the following simple rules –
Right Hand Thumb Rule: According to this rule if a straight current carrying conductor is held in the right hand such that the thumb of the hand represents the direction of current flow, then the direction of folding fingers will represent the direction of magnetic lines of force.
Right Hand Thumb Rule of Circular Currents: According to this rule, if the direction of current in a circular conducting coil is the direction of folding fingers of the right hand, then the direction of the magnetic field will be in the direction of the stretched thumb.
Magnetic field due to an arc shaped conductor which subtends a reflex angle $\theta$ at the center is given by,
$B = \dfrac{{{\mu _O}}}{{4\pi }}\dfrac{{\left( {2\pi - \theta } \right)i}}{r}$
Now for the above question,

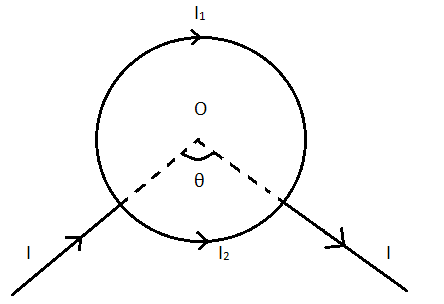
The angle which ${I_2}$ makes at $O = \theta$
The angle which ${I_1}$ makes at $O = 2\pi - \theta$. So,
$\dfrac{{{I_1}}}{{{I_2}}} = \dfrac{{2\pi - \theta }}{\theta }$
${I_1}\left( \theta \right) = {I_2}\left( {2\pi - \theta } \right)$ . . . . . . . . . (1)
Now,
${B_1} = \dfrac{{{\mu _O}}}{{4\pi }}\dfrac{{{I_1}\left( \theta \right)}}{r}$
${B_2} = \dfrac{{{\mu _O}}}{{4\pi }}\dfrac{{{I_2}\left( {2\pi - \theta } \right)}}{r}$
Now, according to the equation (1),
${B_2} = \dfrac{{{\mu _O}}}{{4\pi }}\dfrac{{{I_1}\left( \theta \right)}}{r}$ . . . . $\left[ {\because {I_2}\left( {2\pi - \theta } \right) = {I_1}\left( \theta \right)} \right]$
$\Rightarrow {B_2} = {B_1}$
So the magnitudes of the magnetic fields caused by both the currents is equal. For their directions, we use the right hand thumb rule.
Let’s assume that the coil exists in an $x - y$ plane. So the magnetic field at $O$ due to ${I_1}$ will be in the direction of $\left( { - \hat k} \right)$. And the magnetic field at $O$ due to ${I_2}$ will be in the direction of $\left( {\hat k} \right)$.
So, $\overrightarrow {{B_1}}$ and $\overrightarrow {{B_2}}$ are two vectors which are equal in magnitude but opposite in direction. So their net resultant becomes zero. Therefore, the magnetic field at the center of the circular coil in the figure is zero.

Note :
The above condition is true for all the values of $\theta$. The magnetic field inside a current carrying conductor is always zero, because according to the Biot-Savart’s Law,
$\vec B = \dfrac{{{\mu _O}i}}{{4\pi }}\int {\dfrac{{dl\sin \theta }}{{{r^2}}}\hat n}$.
Now inside the conductor, $\theta = 0$ or $\theta = \pi$. So $\sin \theta$ for these values is zero. And hence the magnetic field inside a conductor is zero.