Question

Show that the locus of the poles of chords which subtend a constant angle a at the vertex is the curve,
${{\left( x+4a \right)}^{2}}=4{{\cot }^{2}}a\left( {{y}^{2}}-4ax \right)$
If the constant angle be a right angle the locus is a straight line perpendicular to the axis.

Answer 1

This question can be solved by writing the equation of the chord joining two points on the parabola and using the formula of angle subtended by a chord on its vertex.
On the parabola ${{y}^{2}}=4ax$, a point can be assumed having coordinates $\left( a{{t}^{2}},2at \right)$ where ‘t’ is a parameter.

Complete step-by-step answer:
Let us assume two points on a parabola ${{y}^{2}}=4ax$ $A\left( at_{1}^{2},2a{{t}_{1}} \right)\ and\ B\left( at_{2}^{2},2a{{t}_{2}} \right)$.
The equation of chord joining points $\left( at_{1}^{2},2a{{t}_{1}} \right)\ and\ \left( at_{2}^{2},2a{{t}_{2}} \right)$ has the equation,
$\left( y-2a{{t}_{2}} \right)=\dfrac{2a{{t}_{2}}-2a{{t}_{1}}}{at_{2}^{2}-at_{1}^{2}}\times \left( x-at_{2}^{2} \right)$
Equation of a line joining two points $\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)$ is $\left( y-{{y}_{1}} \right)=\left( \dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}} \right)\left( x-{{x}_{1}} \right)$.
So, equation of the line joining $A\left( at_{1}^{2},2a{{t}_{1}} \right)\ and\ B\left( at_{2}^{2},2a{{t}_{2}} \right)$.
$\begin{aligned} & \left( y-2a{{t}_{2}} \right)=\dfrac{2a{{t}_{2}}-2a{{t}_{1}}}{at_{2}^{2}-at_{1}^{2}}\times \left( x-at_{2}^{2} \right) \\\ & \Rightarrow \left( y-2a{{t}_{2}} \right)=\dfrac{2a\left( {{t}_{2}}-{{t}_{1}} \right)}{a\left( {{t}_{2}}-{{t}_{1}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)}\times \left( x-at_{2}^{2} \right) \\\ & \Rightarrow \left( y-2a{{t}_{2}} \right)=\dfrac{2}{{{t}_{2}}+{{t}_{1}}}\times \left( x-at_{2}^{2} \right) \\\ & \Rightarrow \left( y-2a{{t}_{2}} \right)\left( {{t}_{2}}+{{t}_{1}} \right)=2\left( x-at_{2}^{2} \right) \\\ \end{aligned}$

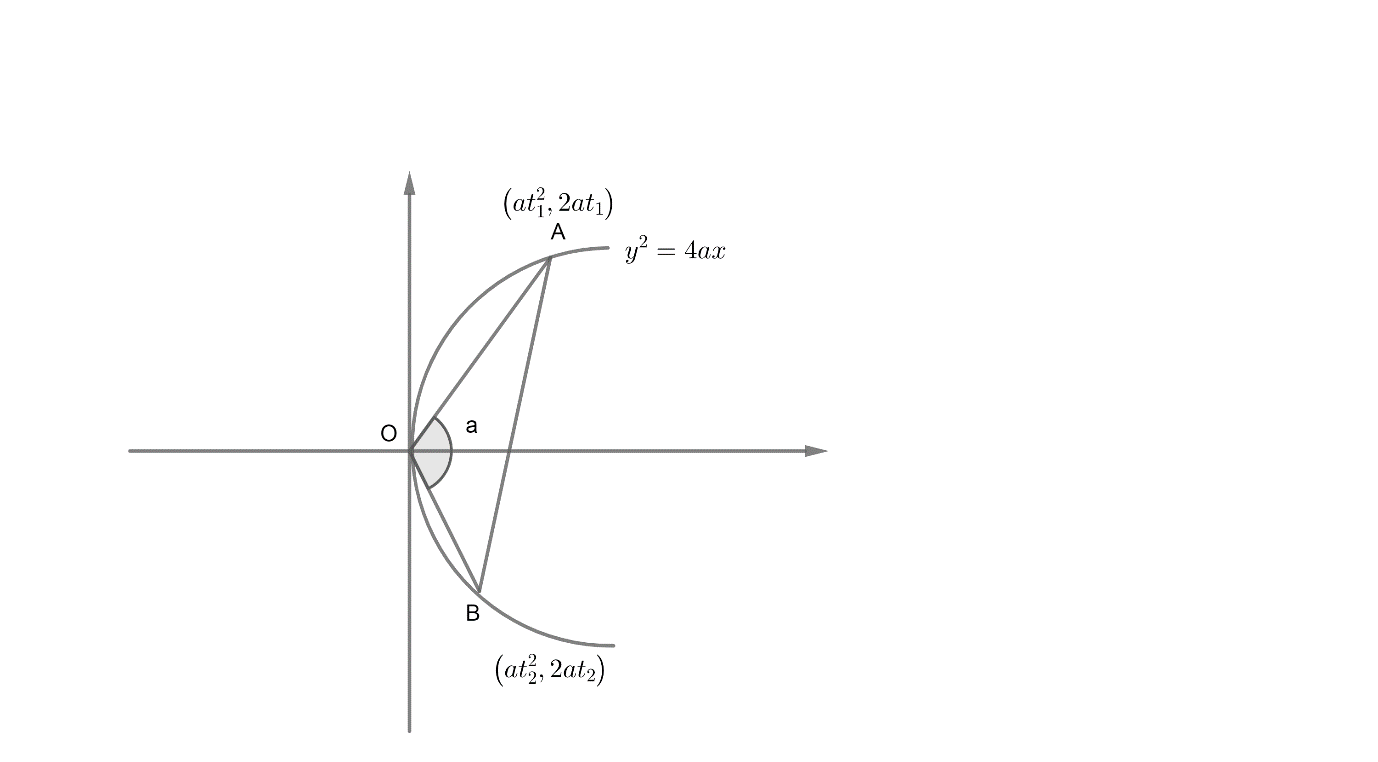
Given the chord subtends angle ‘a’ at the vertex.
Angle between two lines is,
$\begin{aligned} & \tan a=\dfrac{{{m}_{1}}-{{m}_{2}}}{1+{{m}_{1}}{{m}_{2}}} \\\ & where\ {{m}_{1}}=slope\ of\ line\ OA \\\ & {{m}_{2}}=slope\ of\ line\ OB \\\ \end{aligned}$
Slope of line passing through points $\left( {{x}_{1}},{{y}_{1}} \right)\ and\ \left( {{x}_{2}},{{y}_{2}} \right)=\dfrac{{{y}_{2}}-{{y}_{1}}}{{{x}_{2}}-{{x}_{1}}}$
$\begin{aligned} & Slope\ of\ OA=\dfrac{2at_{1}^{2}-0}{at_{1}^{2}-0}=\dfrac{2}{{{t}_{1}}}={{m}_{1}} \\\ & Slope\ of\ OB=\dfrac{2at_{2}^{2}-0}{at_{2}^{2}-0}=\dfrac{2}{{{t}_{2}}}={{m}_{2}} \\\ \end{aligned}$
Comparing the equation $yk=2ax+2ah$ with the equation of the chord, we have,
$\dfrac{{{t}_{1}}+{{t}_{2}}}{k}=\dfrac{2}{2a}=\dfrac{2a{{t}_{1}}{{t}_{2}}}{2ah}...........\left( 2 \right)$
From this equation,
$\begin{aligned} & \Rightarrow h=a{{t}_{1}}{{t}_{2}}\ and \\\ & k=a\left( {{t}_{1}}+{{t}_{2}} \right) \\\ \end{aligned}$
From equation (1) and (2),
$\begin{aligned} & {{t}_{1}}{{t}_{2}}=\dfrac{h}{a}\ and\ \left( {{t}_{1}}+{{t}_{2}} \right)=\dfrac{k}{a} \\\ & Formula:{{\left( a+b \right)}^{2}}-{{\left( a-b \right)}^{2}}=4ab \\\ & {{\left( {{t}_{1}}+{{t}_{2}} \right)}^{2}}-{{\left( {{t}_{1}}-{{t}_{2}} \right)}^{2}}=4{{t}_{1}}{{t}_{2}} \\\ & \Rightarrow \sqrt{\dfrac{{{k}^{2}}}{{{a}^{2}}}-\dfrac{4h}{a}}=\left( {{t}_{1}}-{{t}_{2}} \right) \\\ \end{aligned}$
Equation (1) becomes,
$2\sqrt{\dfrac{{{k}^{2}}}{{{a}^{2}}}-\dfrac{4h}{a}}=\tan a\times \left( 4+\dfrac{h}{a} \right)$
On squaring both sides,
$\begin{aligned} & \Rightarrow 4\left( \dfrac{{{k}^{2}}}{{{a}^{2}}}-\dfrac{4h}{a} \right)={{\tan }^{2}}a{{\left( \dfrac{h}{a}+4 \right)}^{2}} \\\ & \Rightarrow 4\left( \dfrac{{{k}^{2}}-4ah}{{{a}^{2}}} \right)={{\tan }^{2}}a{{\left( \dfrac{h+4a}{a} \right)}^{2}} \\\ & \Rightarrow \dfrac{4\left( {{k}^{2}}-4ah \right)}{{{a}^{2}}}={{\tan }^{2}}a\dfrac{{{\left( h+4a \right)}^{2}}}{{{a}^{2}}} \\\ & \Rightarrow 4\left( {{k}^{2}}-4ah \right)={{\tan }^{2}}a{{\left( h+4a \right)}^{2}} \\\ \end{aligned}$
On replacing ‘h’ with ‘x’ and ‘k’ with ‘y’,
$\begin{aligned} & 4\left( {{y}^{2}}-4ax \right)={{\tan }^{2}}a{{\left( x+4a \right)}^{2}} \\\ & \Rightarrow {{\left( x+4a \right)}^{2}}=\dfrac{4}{{{\tan }^{2}}a}\left( {{y}^{2}}-4ax \right) \\\ & \Rightarrow {{\left( x+4a \right)}^{2}}=4{{\cot }^{2}}a\left( {{y}^{2}}-4ax \right) \\\ \end{aligned}$
Hence, the required locus is: ${{\left( x+4a \right)}^{2}}=4{{\cot }^{2}}a\left( {{y}^{2}}-4ax \right)$
If the constant angle is $90{}^\circ$, then
$\begin{aligned} & \tan a=\tan 90{}^\circ =Not\ defined \\\ & \Rightarrow \cot 90{}^\circ =0 \\\ \end{aligned}$
So, the locus will be ${{\left( x+4a \right)}^{2}}=0$
$\begin{aligned} & \Rightarrow x+4a=0 \\\ & \Rightarrow x=-4a \\\ \end{aligned}$
This is a line perpendicular to the axis.
Hence, the locus will be a straight line perpendicular to the axis when the constant angle will be a right angle.

Note: This is a simple question in which we have to assume points on parabola in parametric form and obtain relation between the parameters from the given information in the question. Be careful while writing the parametric forms and solving the equations.