Question

Show that the line $y=mx$ bisects the angle between the lines $a{{x}^{2}}-2hxy+b{{y}^{2}}=0$ if $h\left( 1-{{m}^{2}} \right)+m\left( a-b \right)=0$ ?

Answer 1

$a{{x}^{2}}-2hxy+b{{y}^{2}}=0$is an equation which represents a pair of lines. So first we are going to assume two lines which represent the above equation with a definite slope for each line. One line will obviously have greater slope than the other. It is given that the line $y=mx$bisects the angle between these two lines. Using the slopes of these lines, we form an equation. Then we are going to apply $\tan$on both sides to get our desired result.

Complete step by step answer:
Now let us assume two lines which are represented by the equation $a{{x}^{2}}+2hxy+b{{y}^{2}}=0$. Let them be $y-{{m}_{1}}x=0$ where ${{m}_{1}}=\tan \alpha$ ,$y-{{m}_{2}}x=0$and ${{m}_{2}}=\tan \beta$.
Let us assume that $y-{{m}_{2}}x=0$has greater slope than $y-{{m}_{1}}x=0$ which implies that $\beta >\alpha$.
We can write it in the following way :
$\Rightarrow a{{x}^{2}}-2hxy+b{{y}^{2}}=\left( y-{{m}_{1}}x \right)\left( y-{{m}_{2}}x \right)$.
Now let us multiply the line equation with each other and then compare.
Upon doing so, we get the following :
$\begin{aligned} & \Rightarrow a{{x}^{2}}-2hxy+b{{y}^{2}}=\left( y-{{m}_{1}}x \right)\left( y-{{m}_{2}}x \right) \\\ & \Rightarrow a{{x}^{2}}-2hxy+b{{y}^{2}}={{y}^{2}}-{{m}_{2}}xy-{{m}_{1}}xy+{{m}_{1}}{{m}_{2}}{{x}^{2}} \\\ & \Rightarrow a{{x}^{2}}-2hxy+b{{y}^{2}}={{y}^{2}}-xy\left( {{m}_{1}}+{{m}_{2}} \right)+{{m}_{1}}{{m}_{2}}{{x}^{2}} \\\ & \Rightarrow \dfrac{a}{b}{{x}^{2}}-\dfrac{2h}{b}xy+{{y}^{2}}={{y}^{2}}-xy\left( {{m}_{1}}+{{m}_{2}} \right)+{{m}_{1}}{{m}_{2}}{{x}^{2}} \\\ \end{aligned}$
Let us first compare the ${{x}^{2}}$ terms.
Upon doing so, we get the following :
$\Rightarrow \dfrac{a}{b}={{m}_{1}}{{m}_{2}}$
Now let us compare the $xy$ terms.
Upon doing so, we get the following :
$\Rightarrow \dfrac{2h}{b}={{m}_{1}}+{{m}_{2}}$
Let us assume the slope of line $y=mx$to be $\theta$. Let us draw these graphs for clarity.

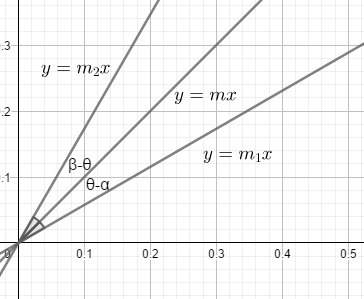
From the figure, the following can deduced :
$\Rightarrow \theta -\alpha =\beta -\theta$ since $y=mx$ bisected the angle between these two lines. So these two have to be equal .
Now let us group the $\theta s$ and apply $\tan$on both sides.
Upon doing so, we get the following :
$\begin{aligned} & \Rightarrow \theta -\alpha =\beta -\theta \\\ & \Rightarrow 2\theta =\alpha +\beta \\\ & \Rightarrow \tan \left( 2\theta \right)=\tan \left( \alpha +\beta \right) \\\ \end{aligned}$
Now let us apply the formulae and expand and use the results that we got above.
$\begin{aligned} & \Rightarrow \theta -\alpha =\beta -\theta \\\ & \Rightarrow 2\theta =\alpha +\beta \\\ & \Rightarrow \tan \left( 2\theta \right)=\tan \left( \alpha +\beta \right) \\\ & \Rightarrow \dfrac{2\tan \theta }{1-{{\tan }^{2}}\theta }=\dfrac{tan\alpha +\tan \beta }{1-\tan \alpha \tan \beta } \\\ \end{aligned}$
$\tan \beta ,\tan \alpha ,\tan \theta$ are the slopes of the lines $y-{{m}_{2}}x=0,y-{{m}_{1}}x=0,y-mx=0$ respectively.
So let us substitute $\tan \beta$ with ${{m}_{2}}$, $\tan \alpha$ with ${{m}_{{}}}$and $\tan \theta$ with $m$.
Upon doing so, we get the following :
$\begin{aligned} & \Rightarrow \theta -\alpha =\beta -\theta \\\ & \Rightarrow 2\theta =\alpha +\beta \\\ & \Rightarrow \tan \left( 2\theta \right)=\tan \left( \alpha +\beta \right) \\\ & \Rightarrow \dfrac{2\tan \theta }{1-{{\tan }^{2}}\theta }=\dfrac{tan\alpha +\tan \beta }{1-\tan \alpha \tan \beta } \\\ & \Rightarrow \dfrac{2m}{1-{{m}^{2}}}=\dfrac{{{m}_{1}}+{{m}_{2}}}{1-{{m}_{1}}{{m}_{2}}} \\\ \end{aligned}$
From above results, we know that $\dfrac{a}{b}={{m}_{1}}{{m}_{2}}$,$\dfrac{2h}{b}={{m}_{1}}+{{m}_{2}}$.
Let us substitute them and solve further.
$\begin{aligned} & \Rightarrow \theta -\alpha =\beta -\theta \\\ & \Rightarrow 2\theta =\alpha +\beta \\\ & \Rightarrow \tan \left( 2\theta \right)=\tan \left( \alpha +\beta \right) \\\ & \Rightarrow \dfrac{2\tan \theta }{1-{{\tan }^{2}}\theta }=\dfrac{tan\alpha +\tan \beta }{1-\tan \alpha \tan \beta } \\\ & \Rightarrow \dfrac{2m}{1-{{m}^{2}}}=\dfrac{{{m}_{1}}+{{m}_{2}}}{1-{{m}_{1}}{{m}_{2}}} \\\ & \Rightarrow \dfrac{2m}{1-{{m}^{2}}}=\dfrac{\dfrac{2h}{b}}{1-\dfrac{a}{b}} \\\ & \Rightarrow \dfrac{2m}{1-{{m}^{2}}}=\dfrac{2h}{b-a} \\\ \end{aligned}$
We got $\dfrac{2m}{1-{{m}^{2}}}=\dfrac{2h}{b-a}$.
We will just cross-multiply this
Upon doing so, we get the following :
$\begin{aligned} & \Rightarrow \dfrac{2m}{1-{{m}^{2}}}=\dfrac{2h}{b-a} \\\ & \Rightarrow m\left( b-a \right)=h\left( 1-{{m}^{2}} \right) \\\ & \Rightarrow h\left( 1-{{m}^{2}} \right)+m\left( a-b \right)=0 \\\ \end{aligned}$
$\therefore$ Hence, the line $y=mx$ bisects the angle between the lines $a{{x}^{2}}-2hxy+b{{y}^{2}}=0$ if $h\left( 1-{{m}^{2}} \right)+m\left( a-b \right)=0$.

Note: Straight lines and pairs of straight lines are lessons with many results. It has many formulae and we need to know that way a result is proved since it will help in later questions. We should remember all the formulae and care must be taken while doing any calculations. These chapters can be clubbed together with other geometry chapters and asked. This can even be asked in permutations and combinations. Thorough practice is required.