Question

Show that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.

Answer 1

In the solution we will use the Midpoint theorem. According to the Midpoint theorem, when line segments join the mid-points of two sides of a triangle then that line segments are parallel to the third side and are half of it.

Complete step-by-step solution
Let us assume $ABCD$ is a quadrilateral where $P$, $Q$, $R$ and $S$ are mid-points on the sides. $AB$, $BC$, $CD$ and $DA$ respectively. The following is the schematic diagram of the quadrilateral.

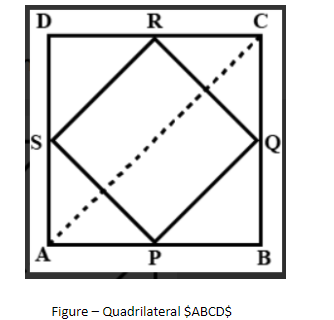
In $\Delta DAC$,
The point $S$ is the midpoint of $DA$ whereas $R$ is the midpoint of $DC$. Therefore,
$SR\parallel AC$ and $SR = \dfrac{1}{2}AC$ ….…(1)
In $\Delta ABC$,
The point $P$ is the midpoint of $AB$ whereas $Q$ is the midpoint of $BC$. Therefore,
$PQ\;\parallel AC$ and $PQ = \dfrac{1}{2}AC$ …….(2)
On comparing equation $\left( 1 \right)$ and equation $\left( 2 \right)$. we get
$PQ = SR$ and $PQ\parallel SR$ ………(3)
From equation $\left( 3 \right)$ it can be concluded that in $PQRS$ one pair of opposite sides is parallel and equal. Hence $PQRS$is a parallelogram.
And, $PR$ and $SQ$ are diagonals of parallelogram $PQRS$.
Therefore, $OP = OR$ and $OQ = OS$ since diagonals of a parallelogram bisect each other.
Therefore, it is proved that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.

Note: Make sure to use the Midpoint theorem when any question is asking about a quadrilateral with midpoints and use Angle Side Angle similar (ASA) triangle properties to compare two triangles.