Question
Question: Show that the length of any focal chord of a conic is a third proportional to the transverse axis an...
Show that the length of any focal chord of a conic is a third proportional to the transverse axis and the diameter parallel to the chord.
Solution
Hint: First of all, consider the general equation of the conic and consider a chord on the conic and find out its length. Convert the obtained fractions into ratio and proportions to prove the problem.
Complete step-by-step answer:
Let the conic be
rl=1−ecosθ
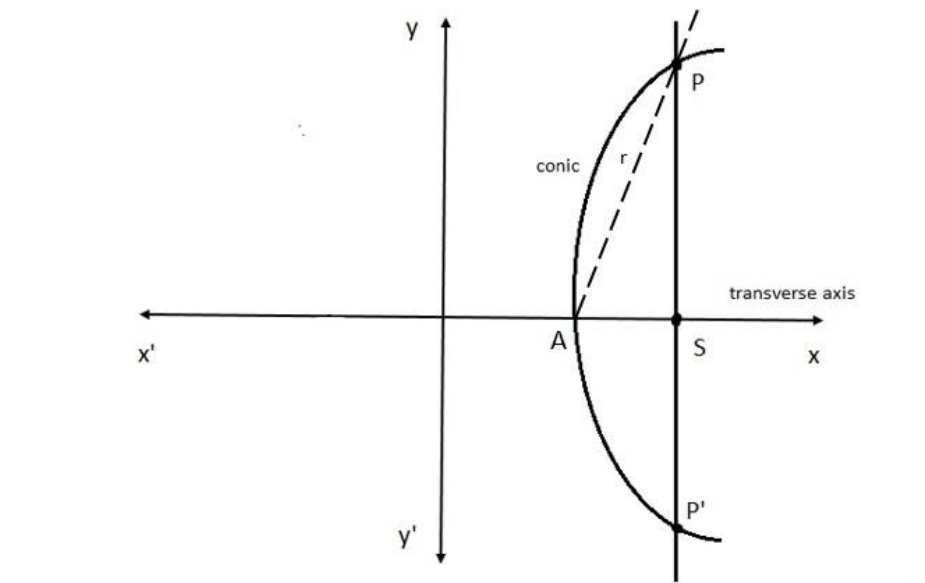
Where ∠PAS=θ
Here r is the radius vector of any point and the diameter through the point (say P) will be 2r.
As we know that r2=b2cos2θ+a2sin2φa2b2 where a is the length of the major axis and b is the length of the minor axis.
Hence
⇒x2=(2r)2=4r2=b2cos2θ+a2sin2θ4a2b2.........................................(1)
Let PSP′ be any chord on the conic then we have
PS=1−ecosθl and P′S=1−ecos(π+θ)l=1+ecosθl
Let the length of the chord PSP′ be y, then we have
Again, in a conic we have
b2=a2(1−e2)
Which can be written as
⇒e2=1−a2b2=a2a2−b2 and 2l=a2b2.............................(3)
Substituting (3) in (2), we get
From equation (1), we have
⇒y=2a1x2 ∴x2=2ay or x2a=yxBy converting these into ratio and proportion, we get
2a:x is in proportion to x:y
i.e., the length of any focal chord of a conic is third proportional to the transverse axis and the diameter parallel to that chord.
Hence proved.
Note: The general equation of a conic is given by rl=1−ecosθ where e is the eccentricity of the conic. Here the point S is the focus of the conic. The transverse axis is the axis of the conic that passes through the two foci.
