Question
Question: Show that the function f(x) = 2x-|x| is continuous at x = 0....
Show that the function f(x) = 2x-|x| is continuous at x = 0.
Solution
Hint: Use the fact that if f(x) is continuous and g(x) is continuous at x= a then so is f(x)+g(x) and f(x)g(x). In the above property take f(x) = 2x and g(x) = -|x|. Use the fact that 2x and –|x| are continuous at x = 0. Alternatively, we can prove that x→0−Limf(x)=x→0+Limf(x)=f(0). Alternatively you can draw a graph of f(x) and verify whether f(x) is continuous at x= 0 or not.
Complete step-by-step answer:
We know that g(x) = 2x is continuous for all real x. Hence g(x) is continuous at x = 0.
Also h(x) = -|x| is continuous for all real x. Hence h(x) is also continuous at x= 0.
Hence g(x)+h(x) is also continuous at x=0.
Hence 2x-|x| is also continuous at x = 0.
Hence f(x) continuous at x=0.
Note: [1] Alternatively, we have
x→0−Limf(x)=x→0−Lim2x−∣x∣
Since for x<0 |x| = -x, we get
x→0−Limf(x)=x→0−Lim2x+x=x→0−Lim3x=0
x→0+Limf(x)=x→0+Lim2x−∣x∣
Since for x>0 |x| = x, we get
x→0+Limf(x)=x→0+Lim2x−x=x→0+Limx=0
f(0) = 2(0)-|0| = 0-0 = 0.
Hence, we have x→0−Limf(x)=x→0+Limf(x)=f(0)
Hence f(x) is continuous at x = 0.
[2] Alternatively, we can draw the graph of f(x) and verify that f(x) is continuous at x = 0
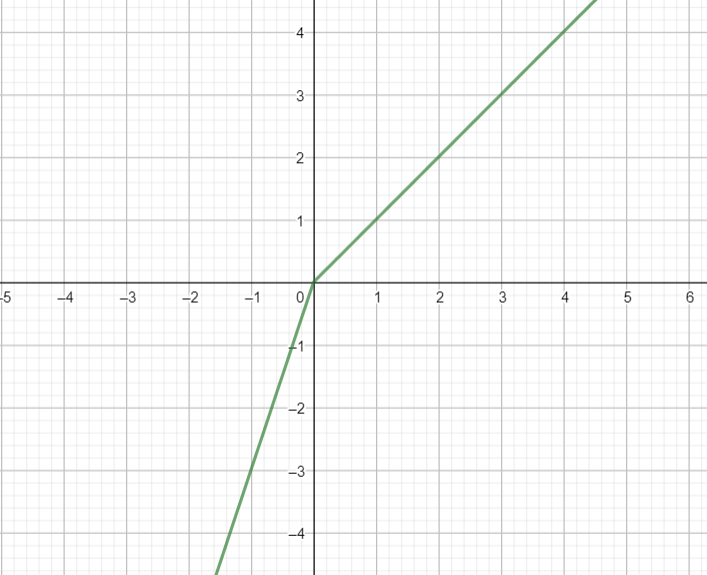
From the graph, it is clear that f(x) is continuous at x=0.
