Question

Show that the function $f:R \cdot \to R \cdot$ defined by $f(x) = \dfrac{1}{x}$ is one-one and onto, where ‘$R \cdot$’ is the set of all non-zero real numbers. Is the result true, if the domain ‘$R \cdot$’ is replaced by $N$ with a co-domain being the same as ‘$R \cdot$’?

Answer 1

To find whether the given function is one-one or not, we will take two elements ${x_1}$ and ${x_2}$ in the set of the domain of the given function and the we will substitute $f\left( {{x_1}} \right) = f\left( {{x_2}} \right)$. If ${x_1} = {x_2}$, then $f(x)$ is a one-one function. To check that the given function is onto or not, we will check if the range of $f(x)$ is equal to the co-domain or not.

Complete step-by-step solution:
It is given that the function is defined for all non-zero real numbers and over all non-zero real numbers. Therefore, both domain and co-domain of the given function consist of the set of all non-zero real numbers.
Assume two elements ${x_1}$ and ${x_2}$ in the set of the domain of the given function. Therefore,
$f\left( {{x_1}} \right) = f\left( {{x_2}} \right)$
Substituting ${x_1}$ and ${x_2}$ in the function, we get
$\Rightarrow \dfrac{1}{{{x_1}}} = \dfrac{1}{{{x_2}}}$
On cross multiplying, we get
$\Rightarrow {x_2} = {x_1}$
On rewriting we get
$\Rightarrow {x_1} = {x_2}$
Hence, we can see that, when $f\left( {{x_1}} \right) = f\left( {{x_2}} \right)$ then ${x_1} = {x_2}$. Therefore, $f$ is one-one.
Now we will check whether $f$ is onto or not.
Given, $f:R \cdot \to R \cdot$ where ‘$R \cdot$’ is the set of all non-zero real numbers defined by $f(x) = \dfrac{1}{x}$.
Let $y = f(x)$, such that $y \in R \cdot$. Therefore, we can write
$\Rightarrow y = \dfrac{1}{x}$
On cross multiplying we get
$\Rightarrow x = \dfrac{1}{y}$
Since, the denominator can’t be zero.
$\therefore y \ne 0$
Therefore, we can say that if y \in R - \left\\{ 0 \right\\}, then x \in R - \left\\{ 0 \right\\} also.
Now, we will check for $y = f(x)$.
Putting the value of $x$ in $f(x)$, we get
$\Rightarrow f(x) = f\left( {\dfrac{1}{y}} \right)$
Substituting $\dfrac{1}{y}$ in the function, we get
$\Rightarrow f(x) = \dfrac{1}{{\dfrac{1}{y}}}$
On simplification,
$\Rightarrow f(x) = y$
Thus, for every $y \in R \cdot$, there exists $x \in R \cdot$ such that $f(x) = y$.
Hence, $f$ is onto.
Now, when the domain $R \cdot$ is replaced by $N$ with co-domain being same as ‘$R \cdot$’
So, we get $f:N \to R \cdot$
Again, we will check if $f:N \to R \cdot$ defined by $f(x) = \dfrac{1}{x}$ is one-one or not.
Assume two elements ${x_1}$ and ${x_2}$ in the set of the domain of the given function. Therefore,
$f\left( {{x_1}} \right) = f\left( {{x_2}} \right)$
Substituting ${x_1}$ and ${x_2}$ in the function, we get
$\Rightarrow \dfrac{1}{{{x_1}}} = \dfrac{1}{{{x_2}}}$
On cross multiplying, we get
$\Rightarrow {x_2} = {x_1}$
On rewriting we get
$\Rightarrow {x_1} = {x_2}$
Hence, we can see that, when $f\left( {{x_1}} \right) = f\left( {{x_2}} \right)$ then ${x_1} = {x_2}$. Therefore, $f$ is one-one.
Now, we will check that $f$ is onto or not.
We have, $f:N \to R \cdot$ defined by $f(x) = \dfrac{1}{x}$.
Let $y = f(x)$, such that $y \in R \cdot$. Therefore, we can write
$\Rightarrow y = \dfrac{1}{x}$
On cross multiplying we get
$\Rightarrow x = \dfrac{1}{y}$
Here, $x$ cannot always be a natural number because $y$ is a real number except zero.
For example, let $y = 3$ then $x = \dfrac{1}{3}$, which is not a natural number.
Hence, $f$ is not onto.

Note: We can also show that $f:R \cdot \to R \cdot$ defined by $f(x) = \dfrac{1}{x}$ is onto by a graphical method.
Consider the graph of $f(x) = \dfrac{1}{x}$ as shown below,

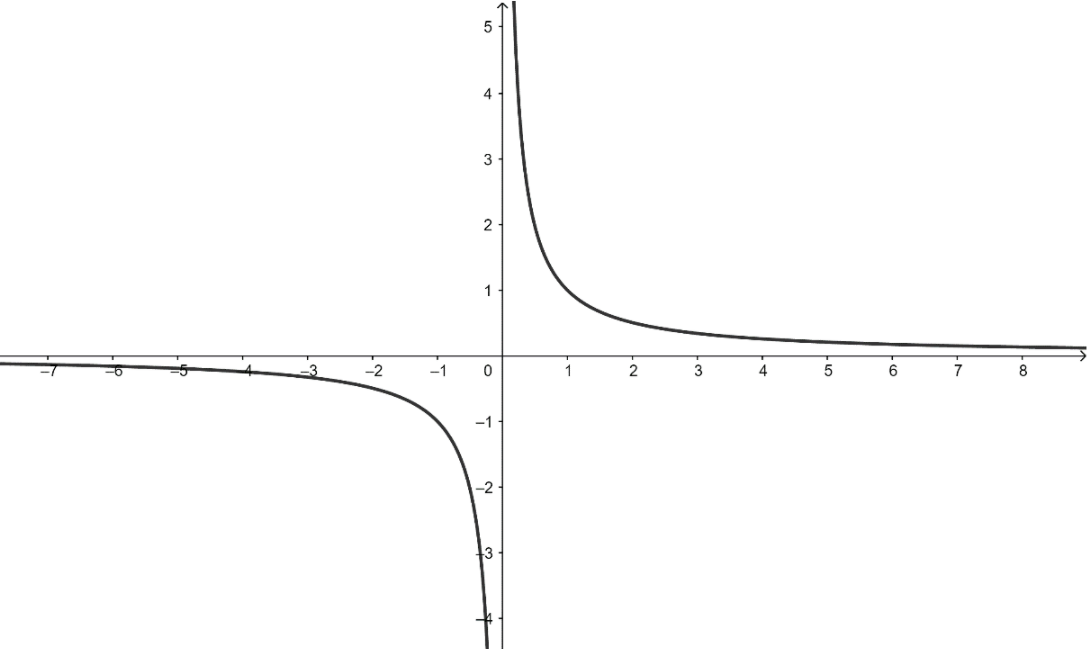
Clearly, we can see that the range of the function $f:R \cdot \to R \cdot$ defined by $f(x) = \dfrac{1}{x}$ is R - \left\\{ 0 \right\\}.
The range of the given function is all real numbers except zero. Hence, the range and codomain of the function are equal.
Therefore, $f$ is not onto.