Question

Show that the function $f\left( x \right)=\sin x$ is

& \text{a) strictly increasing in }\left( 0,\dfrac{\pi }{2} \right) \\\ & \text{b) strictly decreasing in }\left( \dfrac{\pi }{2},\pi \right) \\\ & \text{c) neither increasing nor decreasing in (0,}\pi ) \\\ \end{aligned}$$

Answer 1

Now we are given with the function $f\left( x \right)=\sin x$ . We will differentiate the function and find $f'\left( x \right)$ . Now f(x) is increasing if f’(x) > 0 and f(x) is decreasing if f’(x) < 0. Hence we will check the nature of f’(x) in the intervals to arrive at required conclusions.

Complete step-by-step solution:
Now the given function is a well-known trigonometric function sin x.
Now let us first understand the concept of increasing functions and decreasing functions.
Now as the name suggests increasing functions are the functions whose value increases as we increase x. Hence increasing functions are the functions for which we have whenever ${{x}_{1}}> {{x}_{2}}$ we have $f({{x}_{1}}) >f({{x}_{2}})$ . Similarly decreasing function is the function whose value decreases with increase in c hence for a decreasing functions we have whenever ${{x}_{1}}> {{x}_{2}}$ we have $f({{x}_{1}})< f({{x}_{2}})$ . Now, this can be possible that the function increases in one interval and decreases in another interval. Then the function is neither increasing nor decreasing. But we can specify the intervals in which it is increasing, not decreasing.
Now to check the nature of the function f(x) we have the first derivative test.
According to the first derivative test if f(x) is increasing if $f’(x) > 0$ and f(x) is decreasing if $f’(x) < 0.$
Now consider the function $f(x)=\sin x$ . Differentiating with respect to x we get.
$f'(x)=\cos x$
Now let us draw the graph of $\cos x$ for $x\in \left( 0,\pi \right)$

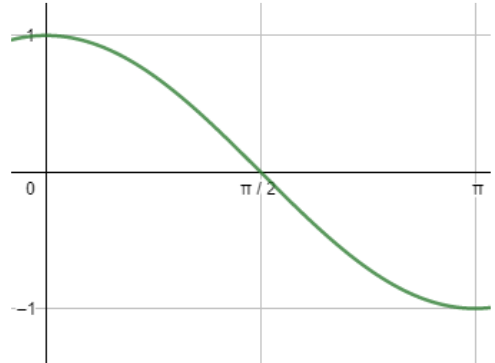
Hence by observing the graph we can say that $\cos x> 0$ for $x\in \left( 0,\dfrac{\pi }{2} \right)$ and $\cos x<0$ for $x\in \left( \dfrac{\pi }{2},\pi \right)$ .
Hence we can say that $\sin x$ is increasing for $x\in \left( 0,\dfrac{\pi }{2} \right)$ and decreasing for $x\in \left( \dfrac{\pi }{2},\pi \right)$ and hence neither decreasing nor increasing for $x\in \left( 0,\pi \right)$ .

Note: Now note that we can also make these conclusions without using the first derivative test. Let us draw the graph of sin x.

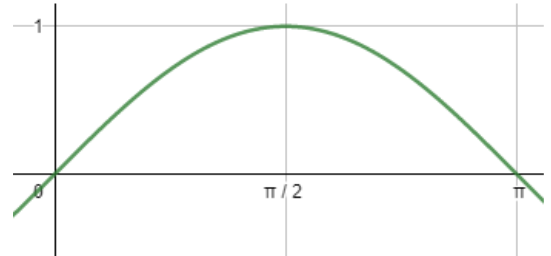
Now we can see that the value of the function increases with x when $x\in \left( 0,\dfrac{\pi }{2} \right)$ and the value of function decreases for $x\in \left( \dfrac{\pi }{2},\pi \right)$ . Hence we can say that $\sin x$ is increasing for $x\in \left( 0,\dfrac{\pi }{2} \right)$ and decreasing for $x\in \left( \dfrac{\pi }{2},\pi \right)$ .