Question

Show that the following four conditions are equivalent:
(i)$A \subset B$
(ii)$A - B = \phi$
(iii)$A \cup B = B$
(iv)$A \cap B = A$

Answer 1

In this question, we need to show that condition (i) is equivalent to (ii), condition (ii) is equivalent to (iii) and condition (iii) is equivalent to (iv). Hence, all the four conditions are equivalent. We can also use the Venn diagrams for practical understanding of the question and prove that all the four conditions are equivalent.

Complete step-by-step answer:
Now, let us assume : \subset \to shows\,{\rm{ a\, symbol\, of\, subset\,}}$$$$A \subset B \to shows\,{\rm{ all\, the\, elements\, of\, A\, are\, present\, in\, B\,}} $U \to is\,{\rm{ the\, universal\, set\,}}{\rm{.}}$
Here ,we will do this question in three steps:
step1 Here, we show condition $A \subset B$ is equivalent to condition $A - B = \phi$.

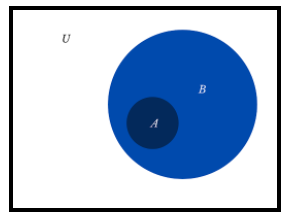
As we know, $A \subset B$ means all the elements of A are present in B.
$\therefore$ B consists of all the elements present in set A.
$\Rightarrow A - B = \phi$
Step2 Here, we show condition $A - B = \phi$ is equivalent to condition $A \cup B = B$.
$A - B = \phi$ means B consists of all the elements present in set A.
As, all the elements of A are present in B.
$\Rightarrow A \cup B = B$
Step3: Here, we show condition $A \cup B = B$ is equivalent to condition $A \cap B = A$.
$A \cup B = B$ means all the elements of A are present in B.
So, all the common elements of A and B must be present in A.
$\Rightarrow A \cap B = A$
Thus, $A \subset B \Leftrightarrow A - B = \phi \Leftrightarrow A \cup B = B \Leftrightarrow A \cap B = A$
Hence, all the four conditions are equivalent to each other.

Additional Information: It is based on set theory which includes collection of unique sets of numbers. There are different types of set operations that are intersection, union, and difference. Based on these operations we draw Venn diagrams related to the need of the question.

Note: The Venn diagrams makes the question easier to understand as well as it helps us to know the concept in an efficient and practical manner. We can easily verify questions by using Venn diagrams as they can be overlapped to check multiple intersections and unions of sets.