Solveeit Logo
Login

Question

Question: Show that the equation \({{x}^{4}}-12{{x}^{2}}+12x-3=0\) has a root between -3 and -4 and another be...

Show that the equation x4−12x2+12x−3=0{{x}^{4}}-12{{x}^{2}}+12x-3=0 has a root between -3 and -4 and another between 2 and 3.

Explanation

Solution

We can find out the solution of the problem using the graph of the equation. We can also use the concept of change of sign of y for a particular domain of x. if the value of y changes in a certain domain then it means that the function has at least one root in that domain.

Complete step-by-step solution:
Let’s assume y=f(x)=x4−12x2+12x−3=0y=f\left( x \right)={{x}^{4}}-12{{x}^{2}}+12x-3=0.
We place the points on the graph to get the figure of the function as

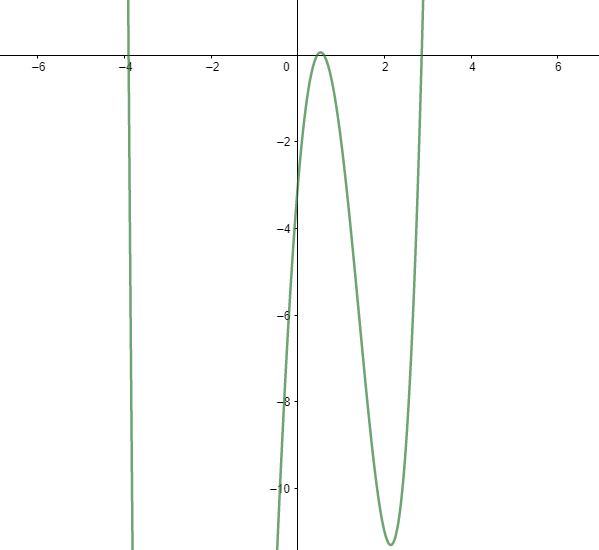
The equation of order 4. So, it should have 4 roots. From the figure, we can see it intersects the y=0y=0 line 4 times.
Now we know for all real values of x the function has a value of y.
So, whenever we put a value of x it either has a positive or a negative sign other than the root values.
So, if the function y=f(x)=x4−12x2+12x−3=0y=f\left( x \right)={{x}^{4}}-12{{x}^{2}}+12x-3=0 changes it signs value inside a range of numbers, that means it has at least one root inside that range.
Now we test it for -3 and -4.
f(−3)=(−3)4−12(−3)2+12(−3)−3=−27−36−3=−66<0f\left( -3 \right)={{\left( -3 \right)}^{4}}-12{{\left( -3 \right)}^{2}}+12\left( -3 \right)-3=-27-36-3=-66<0
f(−4)=(−4)4−12(−4)2+12(−4)−3=64−48−3=13>0f\left( -4 \right)={{\left( -4 \right)}^{4}}-12{{\left( -4 \right)}^{2}}+12\left( -4 \right)-3=64-48-3=13>0
It means the value of y at one point in between (−4,−3)\left( -4,-3 \right) is 0 which indicates that it has a root in (−4,−3)\left( -4,-3 \right).
Similarly, we test it for 2 and 3.
f(2)=(2)4−12(2)2+12(2)−3=−32+24−3=−11<0f\left( 2 \right)={{\left( 2 \right)}^{4}}-12{{\left( 2 \right)}^{2}}+12\left( 2 \right)-3=-32+24-3=-11<0
f(3)=(3)4−12(3)2+12(3)−3=−27+36−3=6>0f\left( 3 \right)={{\left( 3 \right)}^{4}}-12{{\left( 3 \right)}^{2}}+12\left( 3 \right)-3=-27+36-3=6>0
It means the value of y at one point in between (2,3)\left( 2,3 \right) is 0 which indicates that it has a root in (2,3)\left( 2,3 \right).
Thus, prove the equation x4−12x2+12x−3=0{{x}^{4}}-12{{x}^{2}}+12x-3=0 has a root between -3 and -4 and another between 2 and 3.

Note: The concept tells us about the existence of a root is possible or not but it certainly can’t tell about the number of roots of that function in that domain. For that, we obviously need the graph and solution of the equation.