Solveeit Logo
Login

Question

Question: Show that the equation of the line passing through the origin and making an angle \(\theta \) with t...

Show that the equation of the line passing through the origin and making an angle θ\theta with the line y=mx+cy = mx + c is yx=m±tan⁡θ1∓mtan⁡θ\dfrac{y}{x} = \dfrac{{m \pm \tan \theta }}{{1 \mp m\tan \theta }}.

Explanation

Solution

Hint- In this question, we have to find the equation of line passing through origin and making angle θ\theta with the given line. Proceed with using formula of angle θ\theta between two lines of different slopes (m1,m2)({m_1},{m_2}) i.e. tan⁡θ=∣m1−m21+m1m2∣\tan \theta = \left| {\dfrac{{{m_1} - {m_2}}}{{1 + {m_1}{m_2}}}} \right| and find a relation between variables x and y to reach the answer.

Complete step-by-step solution -
__
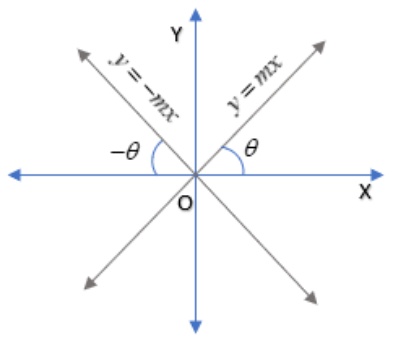
Let equation of the line passing through origin be y=m1xy = {m_1}x ------(a)
Now, this line makes an angle θ\theta with the line y=mx+cy = mx + c
⇒tan⁡θ=∣m1−m1+m1m∣\Rightarrow \tan \theta = \left| {\dfrac{{{m_1} - m}}{{1 + {m_1}m}}} \right|
Put m1=yx{m_1} = \dfrac{y}{x} using the equation (a)
⇒tan⁡θ=±(yx−m1+yx×m)\Rightarrow \tan \theta = \pm \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x} \times m}}} \right)
From this we get, either tan⁡θ=(yx−m1+yx×m)\tan \theta = \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x} \times m}}} \right) or tan⁡θ=−(yx−m1+yx×m)\tan \theta = - \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x} \times m}}} \right)
Taking into consideration, tan⁡θ=(yx−m1+yx×m)\tan \theta = \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x} \times m}}} \right)
On cross multiplying we get, tan⁡θ(1+yx×m)=yx−m\tan \theta \left( {1 + \dfrac{y}{x} \times m} \right) = \dfrac{y}{x} - m
⇒tan⁡θ+tan⁡θ×yx×m=yx−m\Rightarrow \tan \theta + \tan \theta \times \dfrac{y}{x} \times m = \dfrac{y}{x} - m
⇒tan⁡θ+m=yx−tan⁡θ×yx×m\Rightarrow \tan \theta + m = \dfrac{y}{x} - \tan \theta \times \dfrac{y}{x} \times m
⇒tan⁡θ+m=yx(1−mtan⁡θ)\Rightarrow \tan \theta + m = \dfrac{y}{x}\left( {1 - m\tan \theta } \right)
⇒m+tan⁡θ1−mtan⁡θ=yx\Rightarrow \dfrac{{m + \tan \theta }}{{1 - m\tan \theta }} = \dfrac{y}{x}
or, yx=m+tan⁡θ1−mtan⁡θ\dfrac{y}{x} = \dfrac{{m + \tan \theta }}{{1 - m\tan \theta }} ------(b)

Taking into consideration, tan⁡θ=−(yx−m1+yx×m)\tan \theta = - \left( {\dfrac{{\dfrac{y}{x} - m}}{{1 + \dfrac{y}{x} \times m}}} \right)
On cross multiplying we get, tan⁡θ(1+yx×m)=−yx+m\tan \theta \left( {1 + \dfrac{y}{x} \times m} \right) = - \dfrac{y}{x} + m
⇒tan⁡θ+tan⁡θ×yx×m=−yx+m\Rightarrow \tan \theta + \tan \theta \times \dfrac{y}{x} \times m = - \dfrac{y}{x} + m
⇒tan⁡θ−m=−yx−tan⁡θ×yx×m\Rightarrow \tan \theta - m = - \dfrac{y}{x} - \tan \theta \times \dfrac{y}{x} \times m
⇒tan⁡θ−m=yx(−1−mtan⁡θ)\Rightarrow \tan \theta - m = \dfrac{y}{x}\left( { - 1 - m\tan \theta } \right)
⇒tan⁡θ−m−1−mtan⁡θ=yx\Rightarrow \dfrac{{\tan \theta - m}}{{ - 1 - m\tan \theta }} = \dfrac{y}{x}
or, yx=m−tan⁡θ1+mtan⁡θ\dfrac{y}{x} = \dfrac{{m - \tan \theta }}{{1 + m\tan \theta }} ------(c)

From (b) and (c) we get,
yx=m+tan⁡θ1−mtan⁡θ\dfrac{y}{x} = \dfrac{{m + \tan \theta }}{{1 - m\tan \theta }} or yx=m−tan⁡θ1+mtan⁡θ\dfrac{y}{x} = \dfrac{{m - \tan \theta }}{{1 + m\tan \theta }}
Collectively we can say that,
yx=m±tan⁡θ1∓mtan⁡θ\dfrac{y}{x} = \dfrac{{m \pm \tan \theta }}{{1 \mp m\tan \theta }}
Hence it has been shown that yx=m±tan⁡θ1∓mtan⁡θ\dfrac{y}{x} = \dfrac{{m \pm \tan \theta }}{{1 \mp m\tan \theta }}.

Note- Always remember for lines passing through origin, the intercept on y-axis is zero and so in equation y=mx+c,c=0y = mx + c,c = 0 . It can be seen that the line passing through origin can be rewritten as y=mxy = mx where m can be negative or positive depending on the angle.