Question

Show that $\tan \theta \cos \theta = \sin \theta$

Answer 1

Use the basic definitions of tangent, cosine and sine trigonometric functions in order to proof this question. In a right angled triangle, tangent is the ratio of height to base, cosine is the ratio of base to hypotenuse and sine is the ratio of perpendicular to hypotenuse. Use these ratios to prove this problem.

Complete step by step solution:
In order to prove this question, let us understand first, in trigonometry what tangent, cosine and sine function mean?
We can understand this better with the help of a right angled triangle,

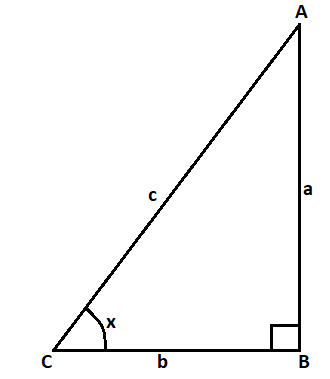
In the $\Delta {\text{ABC}}$ right angled at $\angle {\text{B}}$
${\text{a,}}\;{\text{b}}\;{\text{and}}\;{\text{c}}$ are length of the perpendicular, base and hypotenuse respectively.
And $x$ is the base angle.
Now,
$\sin x$ will be defined as the ratio of perpendicular to hypotenuse, i.e. ${\text{a:c}} = \dfrac{{\text{a}}}{{\text{c}}}$
$\cos x$ will be defined as the ratio of base to hypotenuse, i.e. ${\text{b:c}} = \dfrac{{\text{b}}}{{\text{c}}}$
And $\tan x$ will be defined as the ratio of perpendicular to base, i.e. ${\text{a:b}} = \dfrac{{\text{a}}}{{\text{b}}}$
Now coming to the question, we have to prove the product of tan theta and cos theta is equal to sin theta, we can write it as
$\tan \theta \cos \theta = \sin \theta$
So, in order to proof this, starting simplifying from the left hand side, we will get
${\text{L}}{\text{.H}}{\text{.S}}{\text{.}} = \tan \theta \cos \theta$
Putting respective ratios of $\tan \;{\text{and}}\;\cos$ in the expression

$$\tan \theta \cos \theta = \dfrac{{{\text{perpendicular}}}}{{{\text{base}}}}{ \times }\dfrac{{{\text{base}}}}{{{\text{hypotenuse}}}} \\\ = \dfrac{{{\text{perpendicular}}}}{{{\text{hypotenuse}}}} \\\$$

Now from above elaborations,
$\dfrac{{{\text{perpendicular}}}}{{{\text{hypotenuse}}}} = \sin \theta = {\text{R}}{\text{.H}}{\text{.S}}.$

Note: $\theta$ is the symbolic representation of the word “theta” that is generally used to represent angles. The inverse functions of tangent, cosine and sine functions that are cotangent, secant and cosecant functions respectively, have inverse ratios of their respective inverse functions, an example secant is the ratio of hypotenuse to base whereas cosine has inverse ratio.