Question
Question: Show that \[{\sin ^{ - 1}}\dfrac{{12}}{{13}} + {\cos ^{ - 1}}\dfrac{4}{5} + {\tan ^{ - 1}}\dfrac{{63...
Show that sin−11312+cos−154+tan−11663=π
Solution
Here we will convert all the quantities in terms of tan−1θ first using the trigonometric ratios and then use the following identity to get the desired solution.
tan−1A+tan−1B=tan−1(1−ABA+B)
We will also make use of the pythagoras theorem in the solution.
Complete step-by-step answer:
Let us first consider the left hand side:
LHS=sin−11312+cos−154+tan−11663………………………. (1)
We know that,
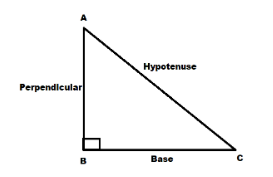
θ=sin−1(hypotenuseperpendicular)
Hence, perpendicular=12
hypotenuse=13
Now according to Pythagoras theorem we know that,
(hypotenuse)2=(base)2+(perpendicular)2
Putting in the respective values we get:-
(13)2=(base)2+(12)2
Simplifying it further we get:-
(base)2=169−144
⇒(base)2=25
Taking square root we get:-
base=5
Now we know that,
θ=tan−1(baseperpendicular)
Putting the values we get:-
θ=tan−1(512)…………………….. (2)
Now we know that,
α=cos−1(hypotenusebase)
Therefore,
base=4
hypotenuse=5
Now according to Pythagoras theorem we know that,
(hypotenuse)2=(base)2+(perpendicular)2
Putting in the respective values we get:-
(5)2=(4)2+(perpendicular)2
Simplifying it further we get:-
(perpendicular)2=25−16
⇒(perpendicular)2=9
Taking square root we get:-
perpendicular=3
Now we know that,
α=tan−1(baseperpendicular)
Putting the values we get:-
α=tan−1(43)……………………………. (3)
Now putting the values from equation 2 and equation 3 in equation 1 we get:-
LHS=tan−1(512)+tan−1(43)+tan−11663
Now applying the following identity for first two terms :-
tan−1A+tan−1B=tan−1(1−ABA+B)
We get:-
LHS=tan−11−(512)(43)512+43+tan−11663
Taking the LCM we get:-
LHS=tan−11−20362012(4)+3(5)+tan−11663
Again taking the LCM in denominator we get:-
LHS=tan−12020−362048+15+tan−11663
Simplifying it further we get:-
LHS=tan−1(−1663)+tan−11663
This implies,
LHS=tan−1(−1663)+tan−11663
Again applying the following identity:-
tan−1A+tan−1B=tan−1(1−ABA+B)
We get:-
LHS=tan−11−(−1663)(1663)−1663+1663
Simplifying it we get:-
LHS=tan−1(1−(−1)0)
⇒LHS=tan−1(20)
⇒LHS=tan−1(0)
Now we know that,
tanπ=0
⇒tan−10=π
Hence, substituting the value we get:-
⇒LHS=π
Now considering RHS we get:-
RHS=π
Hence, LHS=RHS
Hence, proved.
Note: Students should use the trigonometric ratios carefully and convert them using the Pythagoras theorem.
In a right angled triangle,
(hypotenuse)2=(base)2+(perpendicular)2