Question

Show that semi-vertical angle of right circular cone of given surface area and maximum volume a given slant height $l$ is ${{\tan }^{-1}}\left( \dfrac{1}{2\sqrt{2}} \right)$.

Answer 1

Hint: First find the surface area of the cone. After that, take $l=\sqrt{{{h}^{2}}+{{r}^{2}}}$ and compare to get the volume. Then for maximum volume, $\dfrac{dV}{dr}=0$, from this you will get the value of $S$ and substitute in $l$, you will get the value of $l$ in terms of $r$ and also you will get the value of $h$. The take $\tan$ of semi vertical angle and you will get the answer.

Complete step-by-step answer:

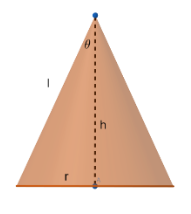
Now the surface area of the cone will be $S=\pi {{r}^{2}}+\pi rl$ where r is the radius and l is the slant height of the cone.
Now $l=\dfrac{S-\pi {{r}^{2}}}{\pi r}$……….. (1)
Also from above figure we know that ${{h}^{2}}+{{r}^{2}}={{l}^{2}}$, where $h$ is the vertical height of the cone.
So we get, $l=\sqrt{{{h}^{2}}+{{r}^{2}}}$ ……….(2)
From (1) and (2), we get,
$\sqrt{{{h}^{2}}+{{r}^{2}}}=\dfrac{S-\pi {{r}^{2}}}{\pi r}$
Squaring both sides we get,

& {{h}^{2}}+{{r}^{2}}={{\left( \dfrac{S-\pi {{r}^{2}}}{\pi r} \right)}^{2}} \\\ & {{h}^{2}}=\left( \dfrac{{{S}^{2}}+{{\pi }^{2}}{{r}^{4}}-2\pi S{{r}^{2}}}{{{\pi }^{2}}{{r}^{2}}} \right)-{{r}^{2}} \\\ & {{h}^{2}}=\left( \dfrac{{{S}^{2}}+{{\pi }^{2}}{{r}^{4}}-2\pi S{{r}^{2}}-{{\pi }^{2}}{{r}^{4}}}{{{\pi }^{2}}{{r}^{2}}} \right) \\\ & {{h}^{2}}=\left( \dfrac{{{S}^{2}}-2\pi S{{r}^{2}}}{{{\pi }^{2}}{{r}^{2}}} \right) \\\ & h=\dfrac{\sqrt{{{S}^{2}}-2\pi S{{r}^{2}}}}{\pi r} \\\ \end{aligned}$$ Now volume of cone V$=\dfrac{1}{3}\pi {{r}^{2}}h=\dfrac{1}{3}\pi {{r}^{2}}\dfrac{\sqrt{{{S}^{2}}-2\pi S{{r}^{2}}}}{\pi r}$ V$=\dfrac{r}{3}\sqrt{{{S}^{2}}-2\pi S{{r}^{2}}}$ For maximum volume, $\dfrac{dV}{dr}=0$. $\begin{aligned} & \dfrac{1}{3}\sqrt{{{S}^{2}}-2\pi S{{r}^{2}}}+\dfrac{r}{3}\dfrac{-4\pi Sr}{2\sqrt{{{S}^{2}}-2\pi S{{r}^{2}}}}=0 \\\ & \dfrac{1}{3}\sqrt{{{S}^{2}}-2\pi S{{r}^{2}}}=\dfrac{r}{3}\dfrac{2\pi Sr}{\sqrt{{{S}^{2}}-2\pi S{{r}^{2}}}} \\\ & {{S}^{2}}=4\pi S{{r}^{2}} \\\ \end{aligned}$ we know that, $S\ne 0$. So $S=4\pi {{r}^{2}}$ Now taking (1) and substituting the $S=4\pi {{r}^{2}}$ we get, $l=\dfrac{4\pi {{r}^{2}}-\pi {{r}^{2}}}{\pi r}=3r$ So $l=\sqrt{{{h}^{2}}+{{r}^{2}}}$ $\begin{aligned} & 9{{r}^{2}}={{h}^{2}}+{{r}^{2}} \\\ & h=2\sqrt{2}r \\\ \end{aligned}$ Now, let $\theta $ be the semi-vertical angle of the cone. $\begin{aligned} & \tan \theta =\dfrac{r}{h}=\dfrac{r}{2\sqrt{2}r} \\\ & \tan \theta =\dfrac{1}{2\sqrt{2}} \\\ \end{aligned}$ So $\theta ={{\tan }^{-1}}\left( \dfrac{1}{2\sqrt{2}} \right)$ Hence proved. Note: This question deals with maxima hence differentiation is involved. Few relations like the one between r, l & h are determined based on the geometry of the figure. For finding the condition for maximum volume, volume is differentiated wrt the radius and equated to 0. Avoid mistakes while differentiating.