Question

Show that $\dfrac{{{{\sin }^3}({{180}^ \circ } + A)\tan ({{360}^ \circ } - A){{\sec }^2}({{180}^ \circ } - A)}}{{{{\cos }^2}({{90}^ \circ } + A)\cos e{c^2}A\sin ({{180}^ \circ } - A)}} = {\tan ^3}A$

Answer 1

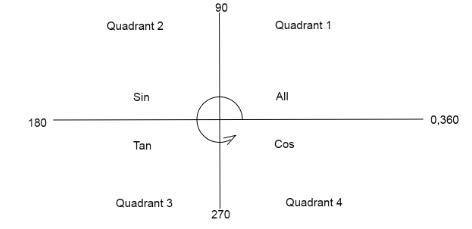
We use the quadrant diagram to find the value of each term in the numerator as well as denominator. Write all values with the same angle ‘A’ and convert all trigonometric functions in simpler forms of ‘sine’ and ‘cosine’.

• $\sec x = \dfrac{1}{{\cos x}};\cos ecx = \dfrac{1}{{\sin x}};\tan x = \dfrac{{\sin x}}{{\cos x}}$
• We know the values of all trigonometric angles are positive in the first quadrant.
  Values of only $\sin \theta$ are positive in the second quadrant.
  Values of only $\tan \theta$ are positive in the third quadrant.
  Values of only $\cos \theta$ are positive in the fourth quadrant.
  

Complete step-by-step answer:
We have to prove $\dfrac{{{{\sin }^3}({{180}^ \circ } + A)\tan ({{360}^ \circ } - A){{\sec }^2}({{180}^ \circ } - A)}}{{{{\cos }^2}({{90}^ \circ } + A)\cos e{c^2}A\sin ({{180}^ \circ } - A)}} = {\tan ^3}A$
We solve for all the trigonometric terms separately.
Terms of numerator:
Since we can write${\sin ^3}({180^ \circ } + A) = {\left[ {\sin ({{180}^ \circ } + A)} \right]^3}$
We will change the angle associated with sine.
Since ${180^ \circ } +$goes to the third quadrant where all $\tan$angles are positive, so all $\sin$angles are negative.
$\Rightarrow {\sin ^3}({180^ \circ } + A) = {\left[ { - \sin A} \right]^3}$
$\Rightarrow {\sin ^3}({180^ \circ } + A) = - {\sin ^3}A$
We have next term as$\tan ({360^ \circ } - A)$
We will change the angle associated with tan.
Since ${360^ \circ } -$goes to the fourth quadrant where all $\cos$angles are positive, so all $\tan$angles are negative.
$\Rightarrow \tan ({360^ \circ } - A) = - \tan A$
Since we can write${\sec ^2}({180^ \circ } - A) = {\left[ {\sec ({{180}^ \circ } - A)} \right]^2}$
We will change the angle associated with secant.
Since ${180^ \circ } -$goes to the second quadrant where all $\sin$angles are positive, so all $\sec$angles are negative.
$\Rightarrow {\sec ^2}({180^ \circ } - A) = {\left[ { - \sec A} \right]^2}$
$\Rightarrow {\sec ^2}({180^ \circ } - A) = {\sec ^2}A$
So the numerator ${\sin ^3}({180^ \circ } + A)\tan ({360^ \circ } - A){\sec ^2}({180^ \circ } - A) = ( - {\sin ^3}A)( - \tan A){\sec ^2}A$
Multiply negative signs together to give a positive sign
$\Rightarrow {\sin ^3}({180^ \circ } + A)\tan ({360^ \circ } - A){\sec ^2}({180^ \circ } - A) = {\sin ^3}A\tan A{\sec ^2}A$...............… (1)
Terms of denominator:
Since we can write${\cos ^2}({90^ \circ } + A) = {\left[ {\cos ({{90}^ \circ } + A)} \right]^2}$
We will change the angle associated with cosine.
Since we know $\cos ({90^ \circ } + A) = - \sin A$
Since ${90^ \circ } +$goes to the third quadrant where all $\tan$angles are positive, so all $\sin$angles are negative.
$\Rightarrow {\cos ^2}({90^ \circ } + A) = {\left[ { - \sin A} \right]^2}$
$\Rightarrow {\cos ^2}({90^ \circ } + A) = {\sin ^2}A$
We have next term as$\sin ({180^ \circ } - A)$
We will change the angle associated with sine.
Since ${180^ \circ } -$goes to the second quadrant where all $\sin$angles are positive.
$\Rightarrow \sin ({180^ \circ } - A) = \sin A$
So the denominator ${\cos ^2}({90^ \circ } + A)\cos e{c^2}A\sin ({180^ \circ } - A) = ( - \sin A)\cos e{c^2}A\sin A$
$\Rightarrow {\cos ^2}({90^ \circ } + A)\cos e{c^2}A\sin ({180^ \circ } - A) = - \sin A\cos e{c^2}A\sin A$...............… (2)
Now we substitute the value of numerator from equation (1) and denominator from equation (2) in the LHS of the equation given in the question.
$\Rightarrow \dfrac{{{{\sin }^3}({{180}^ \circ } + A)\tan ({{360}^ \circ } - A){{\sec }^2}({{180}^ \circ } - A)}}{{{{\cos }^2}({{90}^ \circ } + A)\cos e{c^2}A\sin ({{180}^ \circ } - A)}} = \dfrac{{{{\sin }^3}A\tan A{{\sec }^2}A}}{{{{\sin }^2}A\cos e{c^2}A\sin A}}$.................… (3)
Now we simplify the term by substituting the values of trigonometric functions in terms of sine and cosine.
Substitute $\sec x = \dfrac{1}{{\cos x}};\cos ecx = \dfrac{1}{{\sin x}};\tan x = \dfrac{{\sin x}}{{\cos x}}$
$\Rightarrow \dfrac{{{{\sin }^3}({{180}^ \circ } + A)\tan ({{360}^ \circ } - A){{\sec }^2}({{180}^ \circ } - A)}}{{{{\cos }^2}({{90}^ \circ } + A)\cos e{c^2}A\sin ({{180}^ \circ } - A)}} = \dfrac{{\left( {{{\sin }^3}A} \right)\left( {\dfrac{{\sin A}}{{\cos A}}} \right)\left( {\dfrac{1}{{{{\cos }^2}A}}} \right)}}{{\left( {{{\sin }^2}A} \right)\left( {\dfrac{1}{{{{\sin }^2}A}}} \right)\left( {\sin A} \right)}}$
$\Rightarrow \dfrac{{{{\sin }^3}({{180}^ \circ } + A)\tan ({{360}^ \circ } - A){{\sec }^2}({{180}^ \circ } - A)}}{{{{\cos }^2}({{90}^ \circ } + A)\cos e{c^2}A\sin ({{180}^ \circ } - A)}} = \dfrac{{{{\sin }^3}A \times \sin A \times {{\sin }^2}A}}{{{{\sin }^2}A \times \sin A \times \cos A \times {{\cos }^2}A}}$
Add the powers of terms having same base
$\Rightarrow \dfrac{{{{\sin }^3}({{180}^ \circ } + A)\tan ({{360}^ \circ } - A){{\sec }^2}({{180}^ \circ } - A)}}{{{{\cos }^2}({{90}^ \circ } + A)\cos e{c^2}A\sin ({{180}^ \circ } - A)}} = \dfrac{{{{\sin }^3}A \times {{\sin }^3}A}}{{{{\sin }^3}A{{\cos }^3}A}}$
Cancel same terms from numerator and denominator
$\Rightarrow \dfrac{{{{\sin }^3}({{180}^ \circ } + A)\tan ({{360}^ \circ } - A){{\sec }^2}({{180}^ \circ } - A)}}{{{{\cos }^2}({{90}^ \circ } + A)\cos e{c^2}A\sin ({{180}^ \circ } - A)}} = \dfrac{{{{\sin }^3}A}}{{{{\cos }^3}A}}$
Use law of exponents $\dfrac{{{m^x}}}{{{n^x}}} = {\left( {\dfrac{m}{n}} \right)^x}$ to write the denominator
$\Rightarrow \dfrac{{{{\sin }^3}({{180}^ \circ } + A)\tan ({{360}^ \circ } - A){{\sec }^2}({{180}^ \circ } - A)}}{{{{\cos }^2}({{90}^ \circ } + A)\cos e{c^2}A\sin ({{180}^ \circ } - A)}} = {\left( {\dfrac{{\sin A}}{{\cos A}}} \right)^3}$
Put $\dfrac{{\sin A}}{{\cos A}} = \tan A$
$\Rightarrow \dfrac{{{{\sin }^3}({{180}^ \circ } + A)\tan ({{360}^ \circ } - A){{\sec }^2}({{180}^ \circ } - A)}}{{{{\cos }^2}({{90}^ \circ } + A)\cos e{c^2}A\sin ({{180}^ \circ } - A)}} = {(\tan A)^3}$
$\Rightarrow \dfrac{{{{\sin }^3}({{180}^ \circ } + A)\tan ({{360}^ \circ } - A){{\sec }^2}({{180}^ \circ } - A)}}{{{{\cos }^2}({{90}^ \circ } + A)\cos e{c^2}A\sin ({{180}^ \circ } - A)}} = {\tan ^3}A$
So, LHS is same as RHS
Hence proved.

Note: Students many times make the mistake of proving this question by applying formulas of $\sin (X + Y),\tan (X - Y),\sec (X - Y),\cos (X + Y)$ as per the requirement in LHS. But this is a very complex and confusing long method as we have powers of square and cube which will be applied after using these trigonometric formulas. Equation of each term in numerator will be multiplied to other terms and so on, then taking common factors and cancelling terms will be a very long procedure, so we try to avoid it.
Students are likely to make mistakes while calculating the values from the quadrant diagram, keep in mind that we always move anti-clockwise as we add the angles, so when we subtract the angle we move backwards or clockwise to see which quadrant our function lies in.